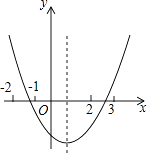题目内容
【题目】已知抛物线y=﹣ ![]() +bx+c与y轴交于点C,与x轴的两个交点分别为A(﹣4,0),B(1,0).
+bx+c与y轴交于点C,与x轴的两个交点分别为A(﹣4,0),B(1,0).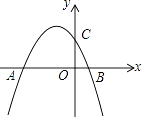
(1)求抛物线的解析式;
(2)已知点P在抛物线上,连接PC,PB,若△PBC是以BC为直角边的直角三角形,求点P的坐标;
(3)已知点E在x轴上,点F在抛物线上,是否存在以A,C,E,F为顶点的四边形是平行四边形?若存在,请直接写出点E的坐标;若不存在,请说明理由.
【答案】
(1)解:抛物线的解析式为y=﹣ ![]() (x+4)(x﹣1),即y=﹣
(x+4)(x﹣1),即y=﹣ ![]() x2﹣
x2﹣ ![]() x+2
x+2
(2)解:存在.
当x=0,y═﹣ ![]() x2﹣
x2﹣ ![]() x+2=2,则C(0,2),
x+2=2,则C(0,2),
∴OC=2,
∵A(﹣4,0),B(1,0),
∴OA=4,OB=1,AB=5,
当∠PCB=90°时,
∵AC2=42+22=20,BC2=22+12=5,AB2=52=25
∴AC2+BC2=AB2
∴△ACB是直角三角形,∠ACB=90°,
∴当点P与点A重合时,△PBC是以BC为直角边的直角三角形,此时P点坐标为(﹣4,0);
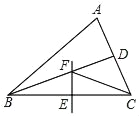
当∠PBC=90°时,PB∥AC,如图1,
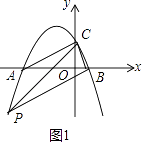
设直线AC的解析式为y=mx+n,
把A(﹣4,0),C(0,2)代入得 ![]() ,解得
,解得 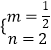 ,
,
∴直线AC的解析式为y= ![]() x+2,
x+2,
∵BP∥AC,
∴直线BP的解析式为y= ![]() x+p,
x+p,
把B(1,0)代入得 ![]() +p=0,解得p=﹣
+p=0,解得p=﹣ ![]() ,
,
∴直线BP的解析式为y= ![]() x﹣
x﹣ ![]() ,
,
解方程组  得
得 ![]() 或
或 ![]() ,此时P点坐标为(﹣5,﹣3);
,此时P点坐标为(﹣5,﹣3);
综上所述,满足条件的P点坐标为(﹣4,0),P2(﹣5,﹣3)
(3)解:存在点E,设点E坐标为(m,0),F(n,﹣ ![]() n2﹣
n2﹣ ![]() n+2)
n+2)

①当AC为边,CF1∥AE1,易知CF1=3,此时E1坐标(﹣7,0),
②当AC为边时,AC∥EF,易知点F纵坐标为﹣2,
∴﹣ ![]() n2﹣
n2﹣ ![]() n+2=﹣2,解得n=
n+2=﹣2,解得n= ![]() ,得到F2(
,得到F2( ![]() ,﹣2),F3(
,﹣2),F3( ![]() ,﹣2),
,﹣2),
根据中点坐标公式得到: ![]() =
= ![]() 或
或 ![]() =
= ![]() ,
,
解得m= ![]() 或
或 ![]() ,
,
此时E2( ![]() ,0),E3(
,0),E3( ![]() ,0),
,0),
③当AC为对角线时,AE4=CF1=3,此时E4(﹣1,0),
综上所述满足条件的点E为(﹣7,0)或(﹣1,0)或( ![]() ,0)或(
,0)或( ![]() ,0)
,0)
【解析】(1)由抛物线经过A(﹣4,0),B(1,0).A、B在x轴上,所以可以设抛物线解析式为两根式:y=![]() (x+4)(x﹣1),展开整理即可;(2)注意分两种情况:①当∠PCB=90°时,②当∠PBC=90°时,不要遗漏情况;(3)分情况讨论:分AC为边,AC为对角线两种情况讨论.
(x+4)(x﹣1),展开整理即可;(2)注意分两种情况:①当∠PCB=90°时,②当∠PBC=90°时,不要遗漏情况;(3)分情况讨论:分AC为边,AC为对角线两种情况讨论.

 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案【题目】某电器超市销售每台进价分别为200元,170元的A,B两种型号的电风扇,表中是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 1800元 |
第二周 | 4台 | 10台 | 3100元 |
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A,B两种型号的电风扇的销售单价.
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,则A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.