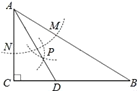
ЬтФПФкШн
ЁОЬтФПЁПШчЭМ1ЃЌЯпЖЮ![]() =12РхУзЃЌЖЏЕу
=12РхУзЃЌЖЏЕу![]() ДгЕу
ДгЕу![]() ГіЗЂЯђЕу
ГіЗЂЯђЕу![]() дЫЖЏЃЌЖЏЕу
дЫЖЏЃЌЖЏЕу![]() ДгЕу
ДгЕу![]() ГіЗЂЯђЕу
ГіЗЂЯђЕу![]()
дЫЖЏЃЌСНЕуЭЌЪБГіЗЂЃЌЕНДяИїздЕФжеЕуКѓЭЃжЙдЫЖЏ.вбжЊЖЏЕу![]() дЫЖЏЕФЫйЖШЪЧЖЏЕу
дЫЖЏЕФЫйЖШЪЧЖЏЕу![]() дЫЖЏЕФЫйЖШЕФ2БЖ.ЩшСНЕужЎМфЕФОрРыЮЊ
дЫЖЏЕФЫйЖШЕФ2БЖ.ЩшСНЕужЎМфЕФОрРыЮЊ![]() (РхУз)ЃЌЖЏЕу
(РхУз)ЃЌЖЏЕу![]() ЕФдЫЖЏЪБМфЮЊ
ЕФдЫЖЏЪБМфЮЊ![]() (Уы)ЃЌЭМ2БэЪО
(Уы)ЃЌЭМ2БэЪО![]() гы
гы![]() жЎМфЕФКЏЪ§ЙиЯЕ.
жЎМфЕФКЏЪ§ЙиЯЕ.
(1)ЧѓЖЏЕу![]() ЁЂ
ЁЂ![]() дЫЖЏЕФЫйЖШ;
дЫЖЏЕФЫйЖШ;
(2)ЭМ2жаЃЌ ![]() = ,
= , ![]() = ,
= , ![]() = ;
= ;
(3)ЕБ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() гы
гы![]() жЎМфЕФКЏЪ§ЙиЯЕЪН(МДЯпЖЮ
жЎМфЕФКЏЪ§ЙиЯЕЪН(МДЯпЖЮ![]() ЖдгІЕФКЏЪ§ЙиЯЕЪН).
ЖдгІЕФКЏЪ§ЙиЯЕЪН).
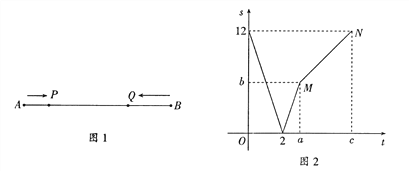
ЁОД№АИЁПЃЈ1ЃЉ2cm/sЃЌ4cm/sЃЛЃЈ2ЃЉ3ЃЌ6ЃЌ6ЃЛЃЈ3ЃЉs=2t(3ЁмtЁм6)
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЯрЯђЖјааЃЌРћгУЫйЖШ![]() ЪБМф=ОрРыСаЪН.(2)РћгУЃЈ1ЃЉЕФНсТлЃЌЖдгІЭМЯѓЧѓНт.(3)ИљОнЭМЯѓжавЛДЮКЏЪ§Й§ЖЈЕуЃЌРћгУД§ЖЈЯЕЪ§ЧѓКЏЪ§НтЮіЪН.
ЪБМф=ОрРыСаЪН.(2)РћгУЃЈ1ЃЉЕФНсТлЃЌЖдгІЭМЯѓЧѓНт.(3)ИљОнЭМЯѓжавЛДЮКЏЪ§Й§ЖЈЕуЃЌРћгУД§ЖЈЯЕЪ§ЧѓКЏЪ§НтЮіЪН.
ЪдЬтНтЮіЃК
ЃЈ1ЃЉЩшЖЏЕуPдЫЖЏЕФЫйЖШЮЊxРхУз/УыЃЌдђЖЏЕуQдЫЖЏЕФЫйЖШЮЊ2xРхУз/УыЃЌ
ИљОнЬтвтЃЌЕУ2ЃЈx+2xЃЉ=12ЃЌ
НтЕУx=2ЃЎ
Д№ЃКЖЏЕуPЁЂQдЫЖЏЕФЫйЖШЗжБ№ЪЧ2РхУз/УыЁЂ4РхУз/УыЃЛ
ЃЈ2ЃЉЖЏЕуQдЫЖЏЕФЪБМфa=![]()
ОЙ§3УыЃЌЖЏЕуQДгЕуBдЫЖЏЕНЕуAЃЌДЫЪБЖЏЕуPдЫЖЏЕФТЗГЬЮЊ2ЁС3=6ЃЌМДb=6ЃЛ
ЖЏЕуPдЫЖЏЕФЪБМфc=![]()
ЙЪД№АИЮЊ3ЃЌ6ЃЌ6ЃЛ
ЃЈ3ЃЉЕБ3ЁмtЁм6ЪБЃЌЩшsгыtжЎМфЕФКЏЪ§ЙиЯЕЪНЮЊs=kt+bЃЌ
ЁпЭМЯѓЙ§ЕуЃЈ3ЃЌ6ЃЉЃЌЃЈ6ЃЌ12ЃЉЃЌЁр![]() ЃЌ
ЃЌ
НтЕУ![]() ,
,
ЁрsгыtжЎМфЕФКЏЪ§ЙиЯЕЪНЮЊs=2tЃЈ3ЁмtЁм6ЃЉЃЎ