题目内容
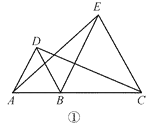
【题目】如图所示,AB⊥BC,CD⊥BC,垂足分别为B、C,AB=BC,E为BC的中点,且AE⊥BD于F,若CD=4cm,则AB的长度为( )

A. 4cm B. 8cm C. 9cm D. 10cm
【答案】B
【解析】∵AB⊥BC,CD⊥BC,
∴∠ABC=∠ACD=90°,
∴∠AEB+∠A=90°.
∵AE⊥BD,
∴∠BFE=90°,
∴∠AEB+∠FBE=90°,
∴∠A=∠FBE,
又∵AB=BC,
∴△ABE≌△BCD,
∴BE=CD=4cm,AB=BC,
∵E为BC的中点,
∴AB=BC=2BE=8cm.
故选B.
点睛:本题考查了等角的余角相等,三角形全等的判定与性质.运用等角的余角相等,得出∠A=∠BFE,从而得到,△ABE≌△BCD是解答本题的关键.

练习册系列答案
相关题目
【题目】在体育课上,对七年级男生进行引体向上测试.以做4个为标准,超过的个数记作正数,不足的个数记作负数其中8名男生做引体向上的个数记录如下:
+3 | -1 | 1 | +3 | 1 | 0 | +2 | -1 |
这8名男生平均每人做了多少个引体向上?