题目内容
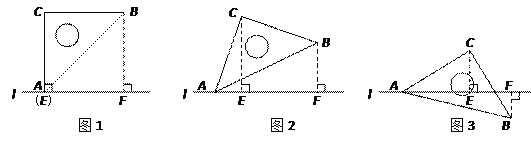
【题目】四边形一条对角线所在直线上的点,如果到这条对角线的两端点的距离不相等,但到另一对角线的两个端点的距离相等,则称这点为这个四边形的准等距点.如图1,点P为四边形ABCD对角线AC所在直线上的一点,PD=PB,PA≠PC,则点P为四边形ABCD的准等距点.

(1)如图2,画出菱形ABCD的一个准等距点.
(2)如图3,在四边形ABCD中,P是AC上的点,PA≠PC,延长BP交CD于点E,延长DP交BC于点F,且∠CDF=∠CBE,CE=CF.求证:点P是四边形ABCD的准等距点.
【答案】(1)见解析;(2)见解析
【解析】
(1)根据菱形的性质,在菱形对角线上找出除中心外的任意一点即可;
(2)连接BD,先利用“角角边”证明△DCF和△BCE全等,根据全等三角形对应边相等可得CD=CB,再根据等边对等角的性质可得∠CDB=∠CBD,从而得到∠PDB=∠PBD,然后根据等角对等边的性质可得PD=PB,根据准等距点的定义即可得证.
(1)如图2,点P即为所画点. (答案不唯一)

(2)证明:连接DB,

在△DCF与△BCE中,
 ,
,
∴△DCF≌△BCE(AAS),
∴CD=CB,
∴∠CDB=∠CBD.
∴∠PDB=∠PBD,
∴PD=PB,
∵PA≠PC
∴点P是四边形ABCD的准等距点.

练习册系列答案
相关题目