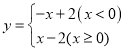题目内容
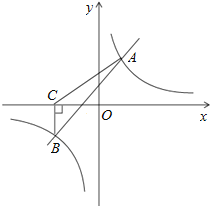
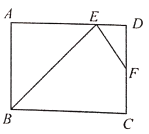
【题目】如图,矩形ABCD中,∠ABC的平分线交AD边于点E,点F是CD的中点,连接EF,若AB=8,且EF平分∠BED,则AD的长为_________
【答案】4+4![]()
【解析】
首先证明AE=AB=8,BE=BG=8![]() ,再证明ED=CG,设AD=BC=x,构建方程即可解决问题.
,再证明ED=CG,设AD=BC=x,构建方程即可解决问题.
解:延长EF交BC的延长线于G.
∵矩形ABCD中,
∴AD∥BC,
∴∠AEB=∠EBC,
∵∠ABC的平分线交AD边于点E,
∴∠ABE=∠EBC,
∴∠ABE=∠AEB,
∴AB=AE=8,
∵∠DEG=∠BEG=∠G,
∴BE=BG=8![]() ,
,
∵DF=FC,∠EDF=∠FCG,∠EFD=∠CFG,
∴△EFD≌△GFC,
∴DE=CG,
设AD=BC=x,则DE=x-8,CG=8![]() -x
-x
∴x-8=8![]() -x,
-x,
解得:x=4+4![]()
即AD=![]() .
.


练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
【题目】已知二次函数y =x2 + 4x + 3.
(1)将二次函数的表达式化为y = a (x-h)2 + k 的形式;
(2)在平面直角坐标系xOy中,用描点法画出这个二次函数的图象;
x | … | … | |||||
y | … | … |
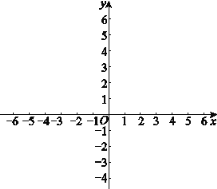
(3)观察图象,直接写出当![]() 时
时![]() 的取值范围;
的取值范围;
(4)根据(2)中的图象,写出一条该二次函数的性质.