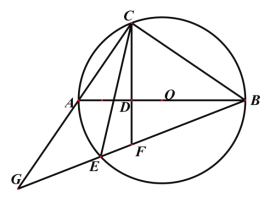
ĢāÄæÄŚČŻ
”¾ĢāÄæ”æ¶ØŅå£ŗ¶ŌÓŚøų¶ØµÄĮ½øöŗÆŹż£¬ČĪČ”×Ō±äĮæxµÄŅ»øöÖµ£¬µ±x£¼0Ź±£¬ĖüĆĒ¶ŌÓ¦µÄŗÆŹżÖµ»„ĪŖĻą·“Źż£»µ±x”Ż0Ź±£¬ĖüĆĒ¶ŌÓ¦µÄŗÆŹżÖµĻąµČ£¬ĪŅĆĒ³ĘÕāŃłµÄĮ½øöŗÆŹż»„ĪŖĻą¹ŲŗÆŹż£®ĄżČē£ŗŅ»“ĪŗÆŹży£½x©2£¬ĖüµÄĻą¹ŲŗÆŹżĪŖ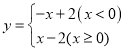
£Ø1£©ŅŃÖŖµćA£Ø©3£¬8£©ŌŚŅ»“ĪŗÆŹży£½ax©5µÄĻą¹ŲŗÆŹżµÄĶ¼ĻóÉĻ£¬ĒóaµÄÖµ£»
£Ø2£©ŅŃÖŖ¶ž“ĪŗÆŹży£½©x2+4x©1£®µ±µćB£Øm£¬2£©ŌŚÕāøöŗÆŹżµÄĻą¹ŲŗÆŹżµÄĶ¼ĻóÉĻŹ±£¬ĒómµÄÖµ£»
”¾“š°ø”æ£Ø1£©1 £Ø2£©![]() »ņ
»ņ![]() »ņ
»ņ![]()
”¾½āĪö”æ
£Ø1£©µ±x<0Ź±£¬y=ax-5µÄĻą¹ŲŗÆŹżĪŖy=©ax+5£¬Č»ŗ󽫵ćA×ų±ź“śČėĒóÖµ¼“æÉ”£
£Ø2£©µ±µćB£Øm£¬2£©ŌŚµÄĻą¹ŲŗÆŹżÉĻŹ±£¬ÓÉÓŚmµÄÖµŹĒ²»Č·¶ØµÄ£¬Ņņ“ĖŅŖ¶ŌmµÄÖµ½ųŠŠ·ÖĄąĢÖĀŪ£¬¼“m<0»ņm”Ż0Į½ÖÖĒéæö£¬Č»ŗóøł¾Ż¶ŌÓ¦µÄĻą¹ŲŗÆŹż½āĪöŹ½£¬ĮīŗÆŹżÖµy=2½ųŠŠĒó½ā¼“æÉ£»
½ā£ŗ£Ø1£©y£½ax©5µÄĻą¹ŲŗÆŹży£½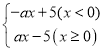 £¬
£¬
½«A£Ø©3£¬8£©“śČėy£½©ax+5µĆ£ŗ3a+5£½8£¬
½āµĆa£½1£»
£Ø2£©¶ž“ĪŗÆŹży£½©x2+4x©1µÄĻą¹ŲŗÆŹżĪŖy£½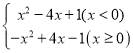 £¬
£¬
µ±m£¼0Ź±£¬½«B£Øm£¬2£©“śČėy£½x2©4x+1µĆ£ŗm2©4m+1£½2£¬
½āµĆ£ŗm£½2+![]() £ØÉįČ„£©£¬»ņm£½2©
£ØÉįČ„£©£¬»ņm£½2©![]() £¬
£¬
µ±m”Ż0Ź±£¬½«B£Øm£¬2£©“śČėy£½©x2+4x©1µĆ£ŗ©m2+4m©1£½2£¬
½āµĆ£ŗm£½2+![]() »ņm£½2©
»ņm£½2©![]() £®
£®
×ŪÉĻĖłŹö£ŗm£½2©![]() »ņm£½2+
»ņm£½2+![]() »ņm£½2©
»ņm£½2©![]() £®
£®

 Õć½Ö®ŠĒæĪŹ±ÓÅ»Æ×÷ŅµĻµĮŠ“š°ø
Õć½Ö®ŠĒæĪŹ±ÓÅ»Æ×÷ŅµĻµĮŠ“š°ø ¼¤»īĖ¼Ī¬ÓżÓæĪĢĆĻµĮŠ“š°ø
¼¤»īĖ¼Ī¬ÓżÓæĪĢĆĻµĮŠ“š°ø”¾ĢāÄæ”æij×ØĀōµź×¼±ø¹ŗ½ų¼×”¢ŅŅĮ½ÖÖŌĖ¶ÆŠ¬£¬Ęä½ų¼ŪŗĶŹŪ¼ŪČēĻĀ±ķĖłŹ¾”£ŅŃÖŖÓĆ3000ŌŖ¹ŗ½ų¼×ÖÖŌĖ¶ÆŠ¬µÄŹżĮæÓėÓĆ2400ŌŖ¹ŗ½ųŅŅÖÖŌĖ¶ÆŠ¬µÄŹżĮæĻąĶ¬.
ŌĖ¶ÆŠ¬¼Ūøń | ¼× | ŅŅ |
½ų¼ŪŌŖ/Ė«) | m | m-30 |
ŹŪ¼Ū(ŌŖ/Ė«) | 300 | 200 |
(1)ĒómµÄÖµ£»
(2)ŅŖŹ¹¹ŗ½ųµÄ¼×£¬ŅŅĮ½ÖÖŌĖ¶ÆŠ¬¹²200Ė«µÄ×ÜĄūČó²»ÉŁÓŚ21700ŌŖĒŅ²»³¬¹ż22300ŌŖ£¬ĪŹøĆ×ØĀōµźÓŠ¼øÖÖ½ų»õ·½°ø?
(3)ŌŚ(2)µÄĢõ¼žĻĀ£¬×ØĀōµź¾ö¶Ø¶Ō¼×ÖÖŌĖ¶ÆŠ¬ĆæĖ«ÓÅ»Ża(60<a<80)ŌŖ³öŹŪ£¬ŅŅÖÖŌĖ¶ÆŠ¬¼Ūøń²»±ä£¬ÄĒĆ“øĆ×ØĀōµźŅŖ»ńµĆ×ī“óĄūČóÓ¦ČēŗĪ½ų»õ?