题目内容
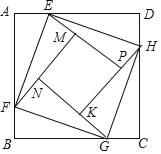
【题目】如图正方形ABCD的边长为2,点E,F,G,H分别在AD,AB,BC,CD上,且EA=FB=GC=HD,分别将△AEF,△BFG,△CGH,△DHE沿EF,FG,GH,HE翻折,得四边形MNKP,设AE=x(0<x<1),S四边形MNKP=y,则y关于x的函数图象大致为( )
A. 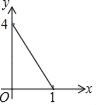 B.
B. 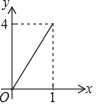 C.
C. 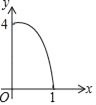 D.
D. 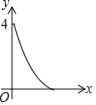
【答案】D
【解析】根据题意和图形,由AE=x(0<x<1),S四边形MNKP=y,得出y=S正方形ABCD-2(S△AEF+S△BGF+S△CGH+S△DEH)2×2﹣2×[![]() x(2﹣x)+
x(2﹣x)+![]() x(2﹣x)+
x(2﹣x)+![]() x(2﹣x)+
x(2﹣x)+![]() x(2﹣x)]=4x2﹣8x+4=4(x﹣1)2,然后根据0<x<1,可得到0<y<4,最后知此函数是二次函数,开口向上,即图象是抛物线,即选项A、B、C错误;选项D符合.
x(2﹣x)]=4x2﹣8x+4=4(x﹣1)2,然后根据0<x<1,可得到0<y<4,最后知此函数是二次函数,开口向上,即图象是抛物线,即选项A、B、C错误;选项D符合.
故选:D.

练习册系列答案
相关题目