题目内容
【题目】如图,抛物线y= ![]() x2+
x2+ ![]() x﹣2与x轴正半轴交于点A,点D(0,m)为y轴正半轴上一点,连结AD并延长交抛物线于点E,若点C(4,n)在抛物线上,且CE∥x轴.
x﹣2与x轴正半轴交于点A,点D(0,m)为y轴正半轴上一点,连结AD并延长交抛物线于点E,若点C(4,n)在抛物线上,且CE∥x轴. 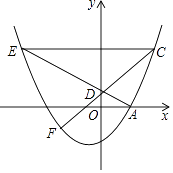
(1)求m,n的值;
(2)连结CD并延长交抛物线于点F,求 ![]() 的值.
的值.
【答案】
(1)解:∵抛物线上x=4时,y= ![]() ×16+
×16+ ![]() ×4﹣2=4,
×4﹣2=4,
∴点C坐标为(4,4),n=4,
∵当y= ![]() x2+
x2+ ![]() x﹣2=4时,解得:x=4或﹣6,
x﹣2=4时,解得:x=4或﹣6,
∴点E坐标为(﹣6,4),
∵当y= ![]() x2+
x2+ ![]() x﹣2=0时,x=2或﹣4,
x﹣2=0时,x=2或﹣4,
∴点A坐标为(2,0),
设直线AE解析式为y=kx+b,则 ![]() ,
,
解得:k=﹣ ![]() ,b=1,
,b=1,
∴直线AE解析式为y=﹣ ![]() x+1,
x+1,
当x=0时,y=1,∴点D坐标为(0,1)
(2)解:设直线CD解析式为y=kx+b,
则代入C、D点得: ![]() ,
,
解得:k= ![]() ,b=1,
,b=1,
∴直线CD解析式为y= ![]() x+1,
x+1,
当y= ![]() x2+
x2+ ![]() x﹣2=
x﹣2= ![]() x+1时,化简得:x2﹣x﹣12=0,
x+1时,化简得:x2﹣x﹣12=0,
解得:x=4或﹣3,
∴点F坐标为(﹣3,﹣ ![]() ),
),
∴DF=  =
= ![]() ,
,
CD= ![]() =5,
=5,
∴ ![]() =
= ![]() =
= ![]()
【解析】(1)将点C横坐标代入抛物线解析式即可求得n的值,根据n的值可以求得点E的坐标,即可求得点A坐标,即可求得直线AE解析式,即可解题;(2)易求得直线CD解析式,即可求得点F坐标,即可求得DF、CD的长,即可解题.
【考点精析】本题主要考查了抛物线与坐标轴的交点的相关知识点,需要掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能正确解答此题.

 口算题天天练系列答案
口算题天天练系列答案【题目】某蔬菜经营户从蔬菜批发市场批发蔬菜进行零售,部分蔬菜批发价格与零售价格如表:
蔬菜品种 | 西红柿 | 青椒 | 西兰花 | 豆角 |
批发价(元/㎏) | 3.6 | 5.4 | 8 | 4.8 |
零售价(元/㎏) | 5.4 | 8.4 | 14 | 7.6 |
请解答下列问题:
(1)第一天,该经营户批发西红柿和西兰花两种蔬菜共300㎏,用去了1520元钱,这两种蔬菜当天全部售完一共赚了多少元钱?
(2)第二天,该经营户用1520元仍然批发西红柿和西兰花,要想当天全部售完后所赚钱数不少于1050元,则该经营户最多能批发西红柿多少㎏?
【题目】中考前的模拟考试对于学生来说具有重大的指导意义,现抽取m名学生的数学一模成绩进行整理分组,形成如下表格(x代表成绩,规定x>140为优秀),并绘制出扇形统计图和频数分布直方图(横坐标表示成绩,单位:分).
A组 | 140<x≤150 |
B组 | 130<x≤140 |
C组 | 120<x≤130 |
D组 | 110<x≤120 |
E组 | 100<x≤110 |
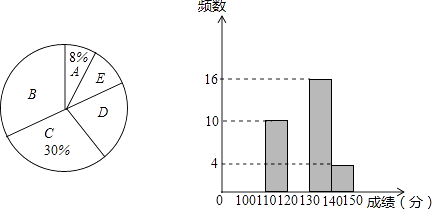
(1)m的值为;扇形统计图中D组对应的圆心角是°.
(2)若要从成绩优秀的学生甲、乙、丙、丁中,随机选出2人介绍经验,求甲、乙两人中至少有1人被选中的概率(通过画树状图或列表法进行分析).