题目内容
【题目】已知：如图，在ABCD中，点F在AB的延长线上，且BF=AB，连接FD，交BC于点E．
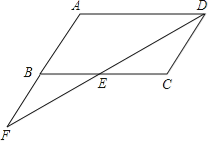
（1）说明△DCE≌△FBE的理由；
（2）若EC=3，求AD的长．
【答案】（1）证明：∵四边形ABCD是平行四边形，
∴AB=DC，AB∥DC
∴∠CDE=∠F
又∵BF=AB
∴DC=FB
在△DCE和△FBE中，
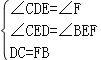
∴△DCE≌△FBE（AAS）
（2）解：∵△DCE≌△FBE，
∴EB=EC，
∵EC=3，
∴BC=2EB=6
∵四边形ABCD是平行四边形，
∴AD=BC=6．
【解析】试题分析：（1）由四边形ABCD是平行四边形，根据平行四边形的对边平行且相等，即可得AB=DC，AB∥DC，继而可求得∠CDE=∠F，又由BF=AB，即可利用AAS，判定△DCE≌△FBE；
（2）由（1），可得BE=EC，即可求得BC的长，又由平行四边形的对边相等，即可求得AD的长．
（1）证明：∵四边形ABCD是平行四边形，
∴AB=DC，AB∥DC，
∴∠CDE=∠F，
又∵BF=AB，
∴DC=FB，
在△DCE和△FBE中，
∵
∴△DCE≌△FBE（AAS）
（2）解：∵△DCE≌△FBE，
∴EB=EC，
∵EC=3，
∴BC=2EB=6，
∵四边形ABCD是平行四边形，
∴AD=BC，
∴AD=6．
练习册系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
【题目】某车间一周内计划每天生产100辆电动车，由于工人实行轮休，每天上班人数不一定相等，实际每天生产量与计划量相比情况如下表（增加的车辆数为正数，减少的车辆数为负数）
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 | ﹣5 | +5 | ﹣5 | +5 | +10 | ﹣10 | ﹣15 |
（1）本周三生产了多少辆电动车？
（2）本周总产量与计划总生产量相比，是增加多少辆？还是减少多少辆？
（3）产量最多的一天比产量最少的一天多生产了多少辆？
（4）请你用折线图画出电动车产量的变化情况．
