��Ŀ����
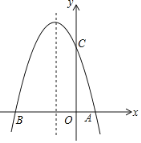
����Ŀ����ͼ����m��������ֱ��l��y����m��y�ύ�ڵ�A��ֱ��a��y��x+m��y�ύ�ڵ�B��������L��y�� x2+mx�Ķ���ΪC����L��x����ΪD��
��1����AB��12����m��ֵ����ʱ�������ߵĶԳ����ϴ���һ���ʹ�á�![]() ���ܳ���С���������ꣻ
���ܳ���С���������ꣻ
��2������C��ֱ��l�Ϸ�ʱ�����C��ֱ��l��������ֵ��
��3����������L��ֱ��a��Χ�ɵķ��ͼ�εı߽��ϣ��Ѻᡢ�����궼�������ĵ��Ϊ�����������ֱ�ֱ��д��m��2020��m��2020.5ʱ���������ĸ�����
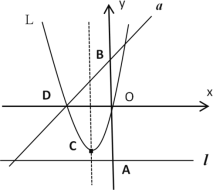
���𰸡���1��P����3��3 ������2����C��l��������ֵΪ1����3��m��2020ʱ���������ĸ���Ϊ4042����m��2020.5ʱ���������ĸ���Ϊ1011��
��������
�⣺��1�����A��B�����꣬�ֱ�ΪA��0����m����B ��0��m������AB��8�����ɵõ�m������m����12���������m.��֪�ϡ���������ڶԳ���Գ�ʱ����OP=DPʱ��OB+OP+PB=OB+DP+PB ��B��P��D������ʱ��![]() �ܳ���̣����P�����꼴��.
�ܳ���̣����P�����꼴��.
��2�������κ���תΪ����ʽ��y����x+ ![]() ��2��
��2��![]() �����������C
�����������C
C��l�ľ���![]() ��1���ݴ˿��жϳ�������.
��1���ݴ˿��жϳ�������.
��3���ֱ������m��2020ʱ���뵱m��2020.5ʱ�����������߽���ʽ��ֱ�߽���ʽ����������꣬�����������µĵ�����������ɣ�ע��������ۡ�
�⣺��1����x��0����y��x+m��m��
��B ��0��m����
��AB��8����A��0����m����
��m������m����12��
��m��6��
��L��y��x2+6x��
��L�ĶԳ���x����3��
��֪�ϡ���������ڶԳ���Գƣ���OP=DP
��OB+OP+PB=OB+DP+PB ��B��P��D������ʱ��![]() �ܳ���̣���ʱ��PΪֱ��a��Գ���Ľ��㣬��x����3����y��x+6��3��
�ܳ���̣���ʱ��PΪֱ��a��Գ���Ľ��㣬��x����3����y��x+6��3��
��P����3��3 ��
��2��y����x+ ![]() ��2��
��2��![]() ��
��
��L�Ķ���C
�ߵ�C��l�Ϸ���
��C��l�ľ���![]() ��1��
��1��
���C��l��������ֵΪ1
��3����m��2020ʱ������4042�����㣬��m��2020.5ʱ������1011�����㡣
�ٵ�m��2020ʱ�������߽���ʽL��y��x2+2020x
ֱ�߽���ʽa��y��x+2020
����������������ʽ�ɵã�x1����2020��x2��1��
���֪ÿһ������x��ֵ ����Ӧ��һ������yֵ���ҩ�2020��1֮�䣨������2020��1������2022��������
������Ҫ֪����Χ�ɵķ��ͼ�α߽�������֣��߶κ������ߣ�
���߶κ��������ϸ���2022��������
���ܼ�4044���㣬
��������ͼ����2�����ظ��ظ���
���������ĸ�����4044��2��4042��������
�ڵ�m��2020.5ʱ��
�����߽���ʽL��y��x2+2020.5x��
ֱ�߽���ʽa��y��x+2020.5��
����������������ʽ�ɵã�x1����2020.5��x2��1��
�൱xȡ����ʱ����һ�κ���y��x+2020.5�ϣ�yȡ��������ֵ������ڸ�ͼ������������Ϊ0��
�ڶ��κ���y��x2+2020.5xͼ���ϣ���xΪż��ʱ������ֵy��ȡ������
��֪��2020.5��1֮����1010��ż���������ک�2020.5��1֮�仹������0����֤���֪0Ҳ����
���������������������1011����
��m��2020ʱ���������ĸ���Ϊ4042����m��2020.5ʱ���������ĸ���Ϊ1011��