题目内容
如图,D是△ABC的边AB上一点且BD=2AD,CD=6,cos∠BCD=
| ||
| 2 |
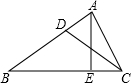
分析:作DF⊥BC于点F,在Rt△CDF中,由CD的长和∠BCD的余弦值,可求DF的长;再根据△BDF∽△BAE,可求AE的长.
解答: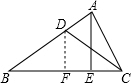 解:过点D作DF⊥BC于点F.
解:过点D作DF⊥BC于点F.
在Rt△CDF中,CD=6,cos∠BCD=
,
∴sin∠BCD=
,DF=CD×sin∠BCD=3.
∵∠B=∠B,∠BFD=∠BEA,
∴△BFD∽△BEA,
∴
=
即:
=
解得:AE=
.
 解:过点D作DF⊥BC于点F.
解:过点D作DF⊥BC于点F.在Rt△CDF中,CD=6,cos∠BCD=
| ||
| 2 |
∴sin∠BCD=
| 1 |
| 2 |
∵∠B=∠B,∠BFD=∠BEA,
∴△BFD∽△BEA,
∴
| AE |
| DF |
| AB |
| BD |
即:
| AE |
| 3 |
| 3 |
| 2 |
解得:AE=
| 9 |
| 2 |
点评:本题考查了在解直角三角形时综合应用三角形相似和特殊三角函数值的能力.

练习册系列答案
相关题目
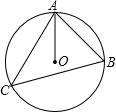 如图,⊙O是△ABC的外接圆,已知∠B=62°,则∠CAO的度数是( )
如图,⊙O是△ABC的外接圆,已知∠B=62°,则∠CAO的度数是( )| A、28° | B、30° | C、31° | D、62° |
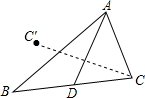 如图,AD是△ABC的中线,∠ADC=60°,点C′与点C关于直线AD对称,若BC=6cm,则点B与点C′之间的距离为
如图,AD是△ABC的中线,∠ADC=60°,点C′与点C关于直线AD对称,若BC=6cm,则点B与点C′之间的距离为 15、如图,AD是△ABC的角平分线,∠B=60°,E,F分别在AC、AB上,且AE=AF,∠CDE=∠BAC,那么,图中长度一定与DE相等的线段共有
15、如图,AD是△ABC的角平分线,∠B=60°,E,F分别在AC、AB上,且AE=AF,∠CDE=∠BAC,那么,图中长度一定与DE相等的线段共有
 如图,⊙O是△ABC的外接圆,AB是直径,若∠B=50°,则∠A等于( )
如图,⊙O是△ABC的外接圆,AB是直径,若∠B=50°,则∠A等于( ) 如图,AD是△ABC的外接圆直径,AD=
如图,AD是△ABC的外接圆直径,AD=