题目内容
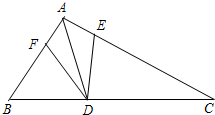 15、如图,AD是△ABC的角平分线,∠B=60°,E,F分别在AC、AB上,且AE=AF,∠CDE=∠BAC,那么,图中长度一定与DE相等的线段共有
15、如图,AD是△ABC的角平分线,∠B=60°,E,F分别在AC、AB上,且AE=AF,∠CDE=∠BAC,那么,图中长度一定与DE相等的线段共有
3
条.分析:先根据SAS证明△AFD≌△AED,所以根据全等三角形的性质知,∠AFD=∠AED,DE=DF;然后由AAA判定△DEC∽△ACB,所以由相似三角形的性质知∠DEC=∠B=60°;再由平角是180°求得∠AFD=∠AED=120°,∠BFD=60°.所以△BDF为等边三角形;最后根据等边三角形的性质解答.
解答:解:在△AFD和△AED中,
∵AD是△ABC的角平分线,
∴∠FAD=∠EAD;
又∵AE=AF,AD=AD(公共边),
∴△AFD≌△AED,(SAS)
∴∠AFD=∠AED,DE=DF;
在△DEC和△ACB中,
又∠CDE=∠BAC,∠C为公共角,
∴△DEC∽△ACB,
∴∠DEC=∠B=60°,
∴∠AFD=∠AED=120°,
∴∠BFD=60°;
又∠B=60°,
∴△BDF为等边三角形,
∴DB=BF=DF=DE.
故答案是:3.
∵AD是△ABC的角平分线,
∴∠FAD=∠EAD;
又∵AE=AF,AD=AD(公共边),
∴△AFD≌△AED,(SAS)
∴∠AFD=∠AED,DE=DF;
在△DEC和△ACB中,
又∠CDE=∠BAC,∠C为公共角,
∴△DEC∽△ACB,
∴∠DEC=∠B=60°,
∴∠AFD=∠AED=120°,
∴∠BFD=60°;
又∠B=60°,
∴△BDF为等边三角形,
∴DB=BF=DF=DE.
故答案是:3.
点评:本题主要考查了全等三角形的判定与性质、相似三角形的判定与性质.解答该题时,一定要挖掘隐含在题设中的已知条件“AD是△ABC的角平分线”,这样,很容易证明△AFD≌△AED.

练习册系列答案
相关题目
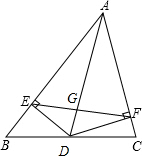 如图,AD是△ABC是角平分线,DE⊥AB于点E,DF⊥AC于点F,连接EF交AD于点G,则AD与EF的位置关系是
如图,AD是△ABC是角平分线,DE⊥AB于点E,DF⊥AC于点F,连接EF交AD于点G,则AD与EF的位置关系是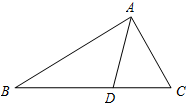 16、已知:如图,AD是△ABC的角平分线,且 AB:AC=3:2,则△ABD与△ACD的面积之比为
16、已知:如图,AD是△ABC的角平分线,且 AB:AC=3:2,则△ABD与△ACD的面积之比为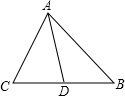 如图,AD是△ABC的边BC上的中线,已知AB=5cm,AC=3cm.
如图,AD是△ABC的边BC上的中线,已知AB=5cm,AC=3cm.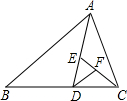 如图,AD是△ABC的中线,CE是△ACD的中线,DF是△CDE的中线,如果△DEF的面积是2,那么△ABC的面积为( )
如图,AD是△ABC的中线,CE是△ACD的中线,DF是△CDE的中线,如果△DEF的面积是2,那么△ABC的面积为( )