题目内容
【题目】如图,在正方形网格中,每个小正方形的边长为1,点A(1,5)、B(6,5)、C(2,3)、D(1,4).
(1)画出△ABC,并判断出△ABC的形状;
(2)将线段AB绕点P逆时针旋转90°得到线段AE,其中点B的对应点为点A,点A的对应点为点E,写出P点的坐标;
(3)连接BD,交AC于点M,则![]() 的比值为 (直接写出结果).
的比值为 (直接写出结果).
【答案】(1)见解析,△ABC是直角三角形;(2)P(![]() ,
,![]() );(3)
);(3)![]()
【解析】
(1)根据勾股定理逆定理即可判断△ABC是直角三角形;
(2)根据题意得出△PAB是等腰直角三角形,进而根据等腰直角三角形的性质求得P的坐标;
(3)通过△BGF∽△BAD,求得GF=![]() ,得到CF=
,得到CF=![]() ,通过证得△ADM∽△CFM,即可求得
,通过证得△ADM∽△CFM,即可求得![]() =
=![]() ,得到
,得到![]() 的比值为
的比值为![]() .
.
解:(1)如图,
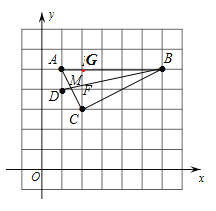
∵点A(1,5)、B(6,5)、C(2,3),
∴AB2=(6﹣1)2+(5﹣5)2=25,AC2=(1﹣2)2+(5﹣3)2=5,BC2=(6﹣2)2+(5﹣3)2=20,
∴AC2+BC2=AB2,
∴△ABC是直角三角形;
(2)∵点B的对应点为点A,
∴P点在AB的垂直平分线上,且∠APB=90°,
∵△PAB是等腰直角三角形,
∴点P到AB的距离为AB的一半,
∵点A(1,5)、B(6,5),
∴点P的横坐标是![]() ,纵坐标是
,纵坐标是![]() ,
,
∴P(![]() ,
,![]() );
);
(3)如图,∵GF//AD,
∴△BGF∽△BAD,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴GF=![]() ,
,
∴CF=2﹣GF=![]() ,
,
∵AD//GC,
∴△ADM∽△CFM,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴![]() 的比值为
的比值为![]() ,
,
故答案为![]() .
.

 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案【题目】已知一个二次函数图象上部分点的横坐标![]() 与纵坐标
与纵坐标![]() 的对应值如表所示:
的对应值如表所示:
| … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
| … | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | … |
(1)求这个二次函数的表达式;
(2)在给定的平面直角坐标系中画出这个二次函数的图象;
(3)当![]() 时,直接写出
时,直接写出![]() 的取值范围.
的取值范围.
【题目】为了了解学生每月的零用钱情况,从甲、乙、丙三个学校各随机抽取200名学生,调查了他们的零用钱情况(单位:元)具体情况如下:
学校频数零用钱 | 100≤x<200 | 200≤x<300 | 300≤x<400 | 400≤x<500 | 500以上 | 合计 |
甲 | 5 | 35 | 150 | 8 | 2 | 200 |
乙 | 16 | 54 | 68 | 52 | 10 | 200 |
丙 | 0 | 10 | 40 | 70 | 80 | 200 |
在调查过程中,从__(填“甲”,“乙”或“丙”)校随机抽取学生,抽到的学生“零用钱不低于300元”的可能性最大.