题目内容
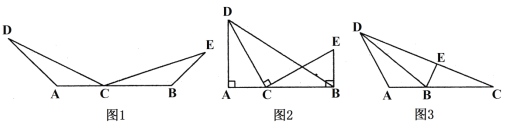
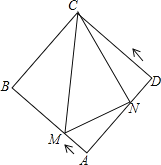
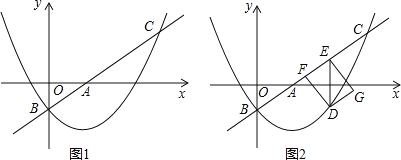
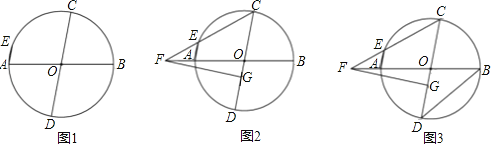
【题目】已知,在⊙O中,AB、CD是直径,弦AE∥CD.
(1)如图1,求证:![]() ;
;
(2)如图2,直线EC与直线AB交于点F,点G在OD上,若FO=FG,求证:△CFG是等腰三角形;
(3)如图3,在(2)的条件下,连接BD,若AE+CD=![]() BD,DG=4,求线段FC的长.
BD,DG=4,求线段FC的长.
【答案】(1)证明见解析;(2)证明见解析;(3)FC=4![]() .
.
【解析】
(1)连接OE,根据平行线的性质以及等腰三角形的性质得出∠EOC=∠COB,从而可得出结果;
(2)连接BC,设∠CBO=α,先根据等腰三角形的性质及对顶角相等求出∠FGO=∠FOG=180°﹣2α,再根据平行线的性质和圆内接四边形的性质得出∠FEA=∠OBC=∠FCD=α,在△FCG中利用三角形的内角和可得出∠CFG=∠FCG=α,最后可得出FG=CG;
(3)连接AC,CB,EO,延长AB至M,使BM=AE,连接CM,过点C作CH⊥AB于H,先利用SAS证明△AEC≌△MBC,得出AC=CM,再由cos∠CAB=![]() =
=![]() =
=![]() ,设AH=3x,AC=4x,进一步可得出
,设AH=3x,AC=4x,进一步可得出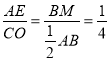 .再由平行得出△AEF∽△OCF,
.再由平行得出△AEF∽△OCF,
有![]() ,再根据线段间的等量关系可求出x的值,从而可得出AC,BC的长,进而得出EC的长,最后根据
,再根据线段间的等量关系可求出x的值,从而可得出AC,BC的长,进而得出EC的长,最后根据![]() 可得出结果.
可得出结果.
(1)证明:连接OE,
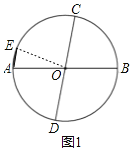
∵AO=EO,
∴∠OAE=∠OEA,
∵AE∥CD,
∴∠OAE=∠COB,∠OEA=∠EOC,
∴∠EOC=∠COB,
∴![]() ;
;
(2)证明:连接BC,设∠CBO=α,
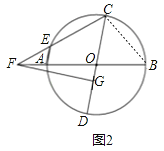
∵OB=OC,
∴∠OCB=∠OBC=α,
∴∠BOC=180°﹣2α,
∴∠FOG=180°﹣2α,
∵FO=FG,
∴∠FGO=∠FOG=180°﹣2α,
∵四边形AECB是圆内接四边形,
∴∠FEA=∠OBC=α,
∵AE∥CD,
∴∠FEA=∠FCD=α,
∴∠CFG=180°﹣∠FCD﹣∠FGC=α,
∴∠CFG=∠FCG=α,
∴FG=CG,
∴△FCG是等腰三角形;
(3)解:如图,连接AC,CB,EO,延长AB至M,使BM=AE,连接CM,过点C作CH⊥AB于H,
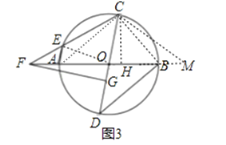
∵AB是直径,
∴∠ACB=90°,
∵∠AOC=∠BOD,
∴AC=BD,
∵AB=CD,AE+CD=![]() BD,
BD,
∴AE+AB=![]() AC,
AC,
∴BM+AB=AM=![]() AC,
AC,
∴![]() ,
,
∵![]() ,
,
∴∠EAC=∠CAB,EC=BC,
∵四边形AECB是圆内接四边形,
∴∠ABC+∠AEC=180°,且∠ABC+∠CBM=180°,
∴∠AEC=∠CBM,且EC=BC,AE=BM,
∴△AEC≌△MBC(SAS),
∴AC=CM,且CH⊥AB,
∴AH=MH=![]() AM,
AM,
∵cos∠CAB=![]() =
=![]() =
=![]() ,
,
∴设AH=3x,AC=4x,则AM=6x,AB=![]() x,
x,
∴BH=AB﹣AH=![]() x,BM=AE=HM﹣BH=
x,BM=AE=HM﹣BH=![]() x,
x,
∴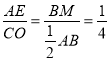 ,
,
∵AE∥CO,
∴△AEF∽△OCF,
∴![]() ,
,
设FA=a,则FO=4a,AO=FO﹣FA=3a,
∵FO=FG=CG=4a,
∴OG=CG﹣CO=a,
∴DG=DO﹣OG=3a﹣a=2a=4,
∴a=2,
∴AO=CO=6,
∴AB=12,
∴![]() x=12,
x=12,
∴x=![]() ,
,
∴AC=9,
∴BC=![]() =
=![]() =3
=3![]() ,
,
∴EC=3![]() ,
,
∵![]() ,
,
∴FC=4![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】为了了解学生每月的零用钱情况,从甲、乙、丙三个学校各随机抽取200名学生,调查了他们的零用钱情况(单位:元)具体情况如下:
学校频数零用钱 | 100≤x<200 | 200≤x<300 | 300≤x<400 | 400≤x<500 | 500以上 | 合计 |
甲 | 5 | 35 | 150 | 8 | 2 | 200 |
乙 | 16 | 54 | 68 | 52 | 10 | 200 |
丙 | 0 | 10 | 40 | 70 | 80 | 200 |
在调查过程中,从__(填“甲”,“乙”或“丙”)校随机抽取学生,抽到的学生“零用钱不低于300元”的可能性最大.