题目内容
【题目】如图,在△ABC中,延长AC至点D,使CD=BC,连接BD,作CE⊥AB于点E,DF⊥BC交BC的延长线于点F,且CE=DF.
(1)求证:AB=AC.
(2)如果∠ABD=105°,求∠A的度数.

【答案】(1)证明见解析;(2)∠A=40°.
【解析】
(1)先由HL判定Rt△BCE≌Rt△CDF,得到∠ABC=∠DCF,然后由对顶角相等可得:∠DCF=∠ACB,进而可得∠ABC=∠ACB,然后由等角对等边,可得AB=AC;
(2)由CD=BC,可得∠CBD=∠CDB,然后由三角形的外角的性质可得:∠ACB=∠CBD+∠CDB=2∠CBD,由∠ABC=∠ACB,进而可得:∠ABC=2∠CBD,然后由∠ABD=∠ABC+∠CBD=3∠CBD=105°,进而可求:∠CBD的度数及∠ABC的度数,然后由三角形的内角和定理即可求∠A的度数.
(1)证明:∵CE⊥AB,DF⊥BC,
∴△BCE和△DCF均是直角三角形,
在Rt△BCE和Rt△DCF中,![]() ,
,
∴Rt△BCE≌Rt△DCF(HL),
∴∠ABC=∠DCF,
∵∠DCF=∠ACB,
∴∠ABC=∠ACB,
∴AB=AC;
(2)解:∵CD=BC,
∴∠CBD=∠CDB,
∵∠ACB=∠CBD+∠CDB,
∴∠ACB=2∠CBD,
∵∠ABC=∠ACB,
∴∠ABC=2∠CBD,
∵∠ABD=∠ABC+∠CBD=3∠CBD=105°,
∴∠CBD=35°,
∴∠ABC=2∠CBD=70°,
∴∠A=180°﹣2∠ABC=40°.

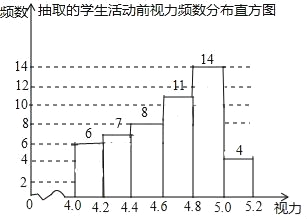
【题目】为了保护视力,某学校开展了全校性的视力保健活动,活动前,随机抽取部分学生,检查他们的视力,结果如图所示,(数据包括左端点不包括右端点,精确到0.1);活动后,再次检查这部分学生的视力,结果如表格所示.
抽取的学生活动后视力频数分布表
分组 | 频数 |
4.0≤x<4.2 | 2 |
4.2≤x<4.4 | 4 |
4.4≤x<4.6 | 6 |
4.6≤x<4.8 | 10 |
4.8≤x<5.0 | 21 |
5.0≤x<5.2 | 7 |
(1)此次调查所抽取的样本容量为 ;
(2)若视力达到4.8以上(含4.8)为达标,请估计活动前该校学生的视力达标率;
(3)请选择适当的统计量,从两个不同的角度分析活动前后相关数据,并评价视力保健活动的效果.

【题目】为了保护视力,某学校开展了全校性的视力保健活动,活动前,随机抽取部分学生,检查他们的视力,结果如图所示,(数据包括左端点不包括右端点,精确到0.1);活动后,再次检查这部分学生的视力,结果如表格所示.
抽取的学生活动后视力频数分布表
分组 | 频数 |
4.0≤x<4.2 | 2 |
4.2≤x<4.4 | 4 |
4.4≤x<4.6 | 6 |
4.6≤x<4.8 | 10 |
4.8≤x<5.0 | 21 |
5.0≤x<5.2 | 7 |
(1)此次调查所抽取的样本容量为 ;
(2)若视力达到4.8以上(含4.8)为达标,请估计活动前该校学生的视力达标率;
(3)请选择适当的统计量,从两个不同的角度分析活动前后相关数据,并评价视力保健活动的效果.