题目内容
【题目】如图,直线PQ∥MN,点A在PQ上,直角△BEF的直角边BE在MN上,且∠B=90°,∠BEF=30°.现将△BEF绕点B以每秒1°的速度按逆时针方向旋转(E,F的对应点分别是E′,F′),同时,射线AQ绕点A以每秒4°的速度按顺时针方向旋转(Q的对应点是Q′).设旋转时间为t秒(0≤t≤45).
(1)∠MBF′=__.(用含t的代数式表示)
(2)在旋转的过程中,若射线AQ′与边E′F′平行时,则t的值为__.

【答案】(90﹣t)°,6°或42°
【解析】
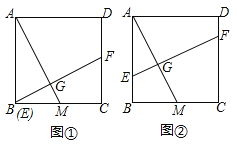
(1)如图1,由题意得:∠FBF'=t°,∠FBM=90°,根据互余的概念进行求解即可得;°;
(2)①如图2、图3,分两种情况分别画出图形进行求解即可得.
(1)如图1,由题意得:∠FBF'=t°,∠FBM=90°,
∴∠MBF'=90°﹣t°=(90﹣t)°,
故答案为:(90﹣t)°;
(2)①如图2,AQ'∥E'F',
延长BE'交AQ'于C,则∠F'E'B=∠ACB=30°,
由题意得:∠EBE'=t°,∠QAQ'=4t°,
∴t+4t=30,
t=6°;
②如图3,AQ'∥E'F',
延长BE',交PQ于D,交直线AQ'于C,则∠F'E'B=∠ACD=30°,
由题意得:∠NBE'=t°,∠QAQ'=4t°,
∴∠ADB=∠NBE'=t°,
∵∠ADB=∠ACD+∠DAC,
∴30+180﹣4t=t,
t=42°,
综上,在旋转的过程中,若射线AQ′与边E′F′平行时,则t的值为6°或42°,
故答案为:6°或42°.

练习册系列答案
相关题目