Question

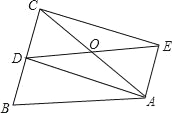
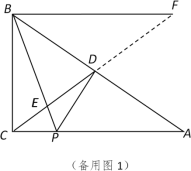
【题目】如图，已知△ABC中，∠ACB＝90°，D是边AB的中点，P是边AC上一动点，BP与CD相交于点E．

（1）如果BC＝6，AC＝8，且P为AC的中点，求线段BE的长；

（2）联结PD，如果PD⊥AB，且CE＝2，ED＝3，求cosA的值；

（3）联结PD，如果BP2＝2CD2，且CE＝2，ED＝3，求线段PD的长．

Answer 1

【答案】（1）（2）(3) .

【解析】

（1）由勾股定理求出BP的长， D是边AB的中点，P为AC的中点，所以点E是△ABC的重心,然后求得BE的长.

（2）过点B作BF∥CA交CD的延长线于点F,所以，然后可求得EF=8，所以，所以，因为PD⊥AB，D是边AB的中点，在△ABC中可求得cosA的值.

（3）由，∠PBD=∠ABP，证得△PBD∽△ABP，再证明△DPE∽△DCP得到，PD可求.

解：（1）∵P为AC的中点，AC=8，

∴CP=4,

∵∠ACB=90°，BC=6，

∴BP=,

∵D是边AB的中点，P为AC的中点，

∴点E是△ABC的重心,

∴,

（2）过点B作BF∥CA交CD的延长线于点F,

∴,

∵BD=DA，

∴FD=DC，BF=AC,

∵CE=2，ED=3，则CD=5，

∴EF=8,

∴,

∴，

∴，设CP=k，则PA=3k，

∵PD⊥AB，D是边AB的中点，

∴PA=PB=3k,

∴，

∴，

∵，

∴,

（3）∵∠ACB=90°，D是边AB的中点，

∴,

∵，

∴,

∵∠PBD=∠ABP，

∴△PBD∽△ABP,

∴∠BPD=∠A,

∵∠A=∠DCA，

∴∠DPE=∠DCP，

∵∠PDE=∠CDP，

△DPE∽△DCP，

∴,

∵DE=3,DC=5，

∴.