题目内容
【题目】函数y=![]() 和y=
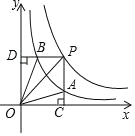
和y=![]() 在第一象限内的图象如图,点P是y=
在第一象限内的图象如图,点P是y=![]() 的图象上一动点,PC⊥x轴于点C,交y=
的图象上一动点,PC⊥x轴于点C,交y=![]() 的图象于点A,PD⊥y轴于点D,交y=
的图象于点A,PD⊥y轴于点D,交y=![]() 的图象于点B.下面结论:
的图象于点B.下面结论:
①PA与PB始终相等;②△OBP与△OAP的面积始终相等;
③四边形PAOB的面积不变;④PABD=PBAC.
其中一定正确的是_____(把你认为正确结论的序号都填上)
【答案】②③④
【解析】
根据反比例函数的图象和性质,特别是根据反比例函数k的几何意义,对四个选项逐一进行分析,即可得出正确答案.
解:∵A、B是反比函数y=![]() 上的点,
上的点,
∴S△OBD=S△OAC=![]() ,
,
∵点P在y=![]() 上,
上,
∴S△PDO=S△POC=![]() ,
,
∴S△POB=S△POA=1,故②正确,
∵当P的横纵坐标相等时PA=PB,故①错误;
∴S四边形PAOB=S△PBO+S△POA=3,故③正确;
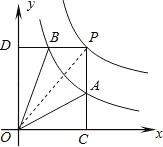
连接OP,
∵![]() =3,
=3,
∴AC=![]() PC,PA=
PC,PA=![]() PC,
PC,
∴![]() =2,
=2,
同理可得![]() =2,
=2,
∴![]() =
=![]() ,即PABD=PBAC故④正确.
,即PABD=PBAC故④正确.
故答案为:②③④.

练习册系列答案
相关题目