Question

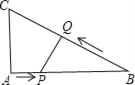
【题目】如图，在△ABC中，AB＝AC，D为BC的中点，四边形ABDE是平行四边形．

（1）求证：四边形ADCE是矩形；

（2）若AC、DE交于点O，四边形ADCE的面积为16，CD＝4，求∠AOD的度数．

Answer 1

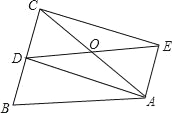
【答案】（1）见解析；（2）∠AOD＝120°

【解析】

（1）已知四边形ABDE是平行四边形，只需证得它的一个内角是直角即可；在等腰△ABC中，AD是底边的中线，根据等腰三角形三线合一的性质即可证得∠ADC是直角，由此得证；

（2）根据矩形的性质得出AD的长度，进而得出∠DAC=30°即可求出答案．

（1）∵四边形ABDE是平行四边形，

∴AE∥BC，AB＝DE，AE＝BD．

∵D为BC中点，

∴CD＝BD．

∴CD∥AE，CD＝AE．

∴四边形ADCE是平行四边形．

∵AB＝AC，D为BC中点，

∴AD⊥BC，即∠ADC＝90°，

∴平行四边形ADCE是矩形；

（2）∵平行四边形ADCE是矩形，四边形ADCE的面积为16，CD＝4，

∴ADCD＝4AD＝16，DO＝AO＝CO＝EO，

解得：AD＝4，

∴tan∠DAC＝，

∴∠DAC＝30°，

∴∠ODA＝30°，

∴∠AOD＝120°．