题目内容
【题目】“若抛物线y=ax2+bx+c与x轴有两个交点,则一元二次方程ax2+bx+c=0有两个不等实根。”请根据你对这句话的理解,解决下面问题:若d、e(d<e)是关于x的方程1+(x﹣f)(x﹣g)=0的两根,且f<g,则d、e、f、g的大小关系是________.
【答案】f<d<e<g
【解析】
依题意画出函数y=(x﹣f)(x﹣g)图象草图,根据二次函数的增减性求解.
解:依题意,画出函数y=(x﹣f)(x﹣g)的图象,如图所示.
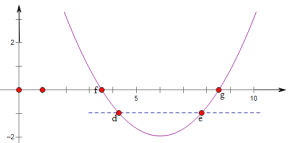
函数图象为抛物线,开口向上,与x轴两个交点的横坐标分别为f,g(f<g).
方程1+(x﹣f)(x﹣g)=0
转化为(x﹣f)(x﹣g)=-1,
方程的两根是抛物线y=(x﹣f)(x﹣g)与直线y=-1的两个交点.
由d<e,可知对称轴左侧交点横坐标为d,右侧为e.
由抛物线开口向上,则在对称轴左侧,y随x增大而减少,则有f<d;在对称轴右侧,y随x增大而增大,则有e<g.
综上所述,可知f<d<e<g.
故答案为:f<d<e<g.

 阅读快车系列答案
阅读快车系列答案【题目】某商场服装部为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励.为了确定一个适当的月销售目标,商场服装部统计了每位营业员在某月的销售额(单位:万元),数据如下:
17 | 18 | 16 | 13 | 24 | 15 | 28 | 26 | 18 | 19 |
22 | 17 | 16 | 19 | 32 | 30 | 16 | 14 | 15 | 26 |
15 | 32 | 23 | 17 | 15 | 15 | 28 | 28 | 16 | 19 |
对这30个数据按组距3进行分组,并整理、描述和分析如下.
频数分布表
组别 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
销售额 |
|
|
|
|
|
|
|
频数 | 7 | 9 | 3 |
| 2 |
| 2 |
数据分析表
平均数 | 众数 | 中位数 |
20.3 |
| 18 |
请根据以上信息解答下列问题:
(1)填空:a= ,b= ,c= ;
(2)若将月销售额不低于25万元确定为销售目标,则有 位营业员获得奖励;
(3)若想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少合适?说明理由.