题目内容
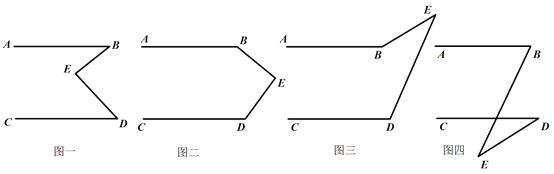
【题目】有一天李明同学用“几何画板”画图,他先画了两条平行线AB,CD,然后在平行线间画了一点E,连接BE,DE后(如图一),他用鼠标左键点住点E,拖动后,分别得到如图二,三,四等图形,这时他突然一想,∠B,∠D与∠BED之间的度数有没有某种联系呢?接着李明同学通过利用“几何画板”的“度量角度”和“计算”功能,找到了这三个角之间的关系.
(1)你能探究出图一到图四各图中的∠B,∠D与∠BED之间的关系吗?
(2)请从所得的四个关系中,选一个说明它成立的理由.
【答案】
如图,
(1)①∠B+∠D=∠BED;
②∠B+∠D+∠BED=360°;
③∠BED=∠D-∠B;
④∠BED=∠B-∠D;
(2)选图③.
过点E作EF∥AB,∵AB∥CD,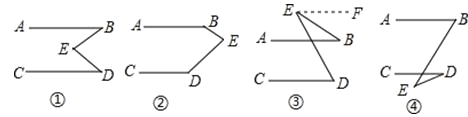
∴EF∥CD,
∴∠D=∠DEF,∠B=∠BEF,
又∵∠BED=∠DEF-∠BEF,
∴∠BED=∠D-∠B.
“点睛”本题考查了平行线的性质,此类题目解题关键在于过拐点作平行线.
【解析】(1)根据两直线平行,内错角相等,两直线平行解答;
(2)选择③,过点E作EF∥AB,根据两直线平行,内错角相等可得∠D=∠DEF,∠B=∠BEF,再根据∠BED=∠DEF-∠BEF整理即可得证.
解:如图,
(1)①∠B+∠D=∠BED;
②∠B+∠D+∠BED=360°;
③∠BED=∠D-∠B;
④∠BED=∠B-∠D;
(2)选图③.
过点E作EF∥AB,∵AB∥CD,
∴EF∥CD,
∴∠D=∠DEF,∠B=∠BEF,
又∵∠BED=∠DEF-∠BEF,
∴∠BED=∠D-∠B.

练习册系列答案
相关题目