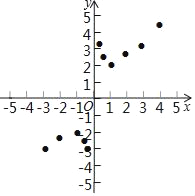题目内容
【题目】益文超市销售某种电器,其成本为每件80元,1月份的销售额为20000元,2月份益文超市对这种电器的售价打9折销售,结果销售量增加了50件,销售额增加了7000元(销售额=销售量×售价).
(1)求该电器1月份的销售单价;
(2)3月份为“献爱心月”,益文超市在1月份的基础上打折促销(但不亏本),销售的数量y(件)与打折的折数x满足一次函数y=﹣50x+600,试求益文超市打几折时利润最大,最大利润是多少?
(3)在(2)的条件下,益文超市发现打n折销售时,3月份的利润与按1月份销售的利润相同,求n的值.
【答案】(1)200元;(2)16000元;(3)n=6.
【解析】
(1)设1月份的销售单价为a元,销量为b件,根据1月的销售额(销售额=销售量×售价)为20000元,2月份商场对这种童装售价打9折销售,结果销售量增加了50件,销售额增加了7000元,列方程组求解即可;
(2)根据利润=销售量×单件利润列函数表达式,根据二次函数性质求最大值;
(3)根据3月份打m折销售时,其利润与原价销售的利润相同,列方程求解.
解:(1)设1月份的销售单价为a元,销量为b件,
则 ab=20000,![]() a(b+50)=27000,
a(b+50)=27000,
解得a=200,b=100.
答:1月份的销售单价为200元.
(2)设利润为W,则W═(![]() ×200﹣80)(﹣50x+600),
×200﹣80)(﹣50x+600),
=﹣1000x2+16000x﹣48000=﹣1000(x﹣8)2+16000,
∵﹣1000<0,
∴当x=8时,W最大,值为16000,
答:当商场打8折时,利润最大,最大利润为16000元;
(3)由(1)知3月份利润为100(200﹣80)=12000元,
依题意:(![]() ×200﹣80)(﹣50n+600)=12000,
×200﹣80)(﹣50n+600)=12000,
解得n1=10(舍),n2=6.

【题目】小明根据学习函数的经验,对函数y=x+![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小明的探究过程,请补充完整:
(1)函数y=x+![]() 的自变量x的取值范围是_____.
的自变量x的取值范围是_____.
(2)下表列出了y与x的几组对应值,请写出m,n的值:m=_____,n=_____;
x | … | ﹣3 | ﹣2 | ﹣1 | ﹣ | ﹣ |
|
| 1 | 2 | 3 | 4 | … |
y | … | ﹣ | ﹣ | ﹣2 | ﹣ | ﹣ | m |
| 2 |
| n |
| … |
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(4)结合函数的图象,请完成:
①当y=﹣![]() 时,x=_____.
时,x=_____.
②写出该函数的一条性质_____.
③若方程x+![]() =t有两个不相等的实数根,则t的取值范围是_____.
=t有两个不相等的实数根,则t的取值范围是_____.