题目内容
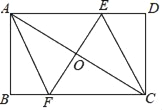
【题目】如图,已知AC是矩形ABCD的对角线,AC的垂直平分线EF分别交BC、AD于点E和F,EF交AC于点O.
(1)求证:四边形AECF是菱形;
(2)若AC=8,EF=6,求菱形的边长.
【答案】(1)证明见解析 (2)5
【解析】
(1)根据对角线垂直的平行四边形是菱形即可判断;
(2)根据勾股定理可求菱形的边长.
(1)∵EF垂直平分AC,
∴OA=OC,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DAC=∠ACB,∠AEO=∠CFO,且OA=OC,
∴△AOE≌△COF(AAS)
∴OE=OF,且OA=OC,
∴四边形AECF是平行四边形,
∵AC⊥EF,
∴四边形AECF是菱形;
(2)∵AC=8,EF=6,
∴OA=OC=4,OE=OF=3,
∵AC⊥EF,
∴AE=![]() =5,
=5,
∴菱形的边长为5.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目