题目内容
【题目】如图，在□ABCD中，AB=2 BC=4，点E、F分别是BC、AD的中点．
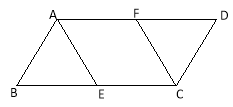
（1）求证：△ABE≌△CDF；
（2）当四边形AECF为菱形时，求出该菱形的面积．
【答案】见试题解析
【解析】
试题分析：（1）根据平行四边形的性质得出AB=CD，∠B=∠D，AD=BC，又因为点E、F分别是BC、AD的中点，所以BE=DF，得出△ABE≌△CDF．（2）取BC的中点G，连接AG，根据菱形的性质得出AE=CE= BE=AB，
∴△ABE是等边三角形. 根据勾股定理求出CG的长，根据面积公式即可求出菱形的面积.
试题解析：（1）证明：在平行四边形ABCD中，点E、F分别是BC、AD的中点，
∴BE=DF, 
,AB=CD，∴△ABE≌△CDF.
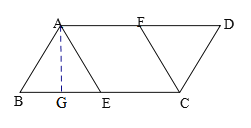
（2）解：取BE的中点G，,连接AG.
当四边形AECF为菱形时，AE=CE= BE=AB，∴△ABE是等边三角形.
又∵EC=2， ∴菱形AECF的面积=EC×AG=2×
=2
.
练习册系列答案
相关题目
