题目内容
【题目】如图，某中学准备用长为20m的篱笆围成一个长方形生物园ABCD饲养小兔，生物园的一面靠墙（围墙MN最长可利用15m），设AB长度为x（m），矩形ABCD面积为y（m2）．
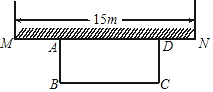
（1）求出y与x的函数关系式，直接写出x的取值范围；
（2）当x为何值时，矩形ABCD的面积最大？最大面积为多少？
【答案】（1）y＝﹣2x2+20x（0＜x≤
）；（2）当x＝5时，面积最大为50m2
【解析】
（1）先表示出长方形的长，然后根据长方形面积=长×宽，表示函数关系式并化简即可；
（2）将函数关系式配方成二次函数顶点式，即确定其最大值.
解：（1）当长方形的宽AB＝x时，其长BC＝20﹣2x，
故长方形的面积y＝x（20﹣2x）＝﹣2x2+20x，
即y＝﹣2x2+20x（0＜x≤）；
（2）y＝﹣2x2+20x
＝﹣2（x﹣5）2+50，
∵﹣2＜0，
∴当x＝5时，y取得最大值，最大值为50，
答：当x＝5时，面积最大为50m2．
练习册系列答案
名校课堂系列答案
相关题目
【题目】若二次函数y=ax2+bx+c的x与y的部分对应值如下表：则下列说法错误的是（ ）
x | … | -1 | 0 | 1 | 2 | 3 | … |
y | … |
|
|
|
|
| … |
A. 二次函数图像与x轴交点有两个
B. x≥2时y随x的增大而增大
C. 二次函数图像与x轴交点横坐标一个在－1~0之间，另一个在2~3之间
D. 对称轴为直线x=1.5
