��Ŀ����
����Ŀ����֪����2��A�ͳ���1��B�ͳ���������һ�ο��˻�10�֣���1��A�ͳ���2��B�ͳ���������һ�ο��˻�11�֣�ij������˾����31�ֻ���ƻ�ͬʱ����A�ͳ�a����B�ͳ�b����һ�����꣬��ǡ��ÿ�������������
����������Ϣ������������⣺
��1��1��A�ͳ���1����B�ͳ�����������һ�οɷֱ��˻����ٶ֣�
��2��������������˾����������
��3����A�ͳ�ÿ�������100Ԫ/�Σ�B�ͳ�ÿ�������120Ԫ/�Σ���ѡ����ʡǮ��������������������ѣ�
���𰸡���1��A�ͳ�װ������һ�ο���3�֣�1��B�ͳ�װ������һ�ο���4�֣�2��3�������������һ��A�ͳ�9����B�ͳ�1����
��������A�ͳ�5����B�ͳ�4����
��������A�ͳ�1����B�ͳ�7����
��3����������A�ͳ�1����B�ͳ�7�����������Ϊ940Ԫ��
��������
�����������1�����ݡ���2��A�ͳ���1��B�ͳ���������һ�ο��˻�10�֣�������1��A�ͳ���2��B�ͳ���������һ�ο��˻�11�֡����ֱ�ó���ʽ���̣���ɷ�����������ɣ�
��2���������������3a+4b=31����˶�Ԫһ�η��̣�����������⣬�õ������������
��3�����ݣ�2��������������A�ͳ�ÿ�������100Ԫ/�Σ�B�ͳ�ÿ�������120Ԫ/�Σ��ֱ��������ü��ɣ�
�⣺��1����ÿ��A�ͳ���B�ͳ���װ������һ�ο��Էֱ��˻�x�֡�y�֣�
�������з�����ã�
![]() ��
��
�ⷽ���飬�ã�![]() ��
��
��1��A�ͳ�װ������һ�ο���3�֣�1��B�ͳ�װ������һ�ο���4�֣�
��2���������ͣ�1���ã�3a+4b=31��
��a=![]()
��a��b����������
��![]() ��
��![]() ��
��![]()
����3���������
����һ��A�ͳ�9����B�ͳ�1����
��������A�ͳ�5����B�ͳ�4����
��������A�ͳ�1����B�ͳ�7����
��3����A�ͳ�ÿ�������100Ԫ/�Σ�B�ͳ�ÿ�������120Ԫ/�Σ�
������һ�����9��100+1��120=1020��Ԫ��
�����������5��100+4��120=980��Ԫ��
�����������1��100+7��120=940��Ԫ��
��1020��980��940
����ʡǮ��������Ƿ�������A�ͳ�1����B�ͳ�7�����������Ϊ940Ԫ��

����Ŀ��������֧����ӽ�����5�������������ɼ����Ƴ���ͳ��ͼ����ͼ��
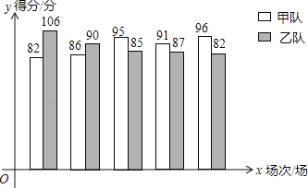
��1���������ͳ��ͼ��д�±�
ƽ���� | ��λ�� | ���� | |
�� | |||
�� |
��2���������������ѡ��һ֧��Ӳμ��������������������ͳ�ƣ���ƽ���֡������Լ���ʤ��������������ֱ���м�Ҫ����������Ϊѡ����֧��Ӳ�������ȡ�úóɼ���
����Ŀ��������9�֣�Ϊ���˽���ͨ��ʱ��������ͨ��ʱ����ָÿ��ͨ��ʱ�䣩�ķֲ������Сǿ�ռ�������1000����ͨ��ʱ�������ݣ���Щ���ݾ�������18����λ�����ӣ��������������ȡ�����ɸ�������Ϊ������ͳ�ƽ�����±����������˲���ɵ�Ƶ���ֲ�ֱ��ͼ��
��ͨ��ʱ���� x/���� | 0��x��3 | 3��x��6 | 6��x��9 | 9��x��12 | 12��x��15 | 15��x��18 |
���� | 36 | a | 8 | 12 | 8 | 12 |
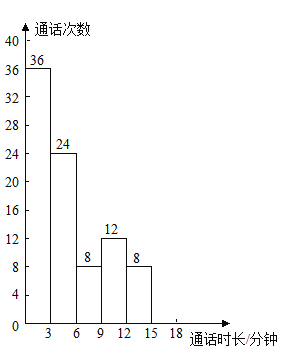
����ͼ�����ṩ����Ϣ������������⣺
��1��a�� ������������ ���������Ƶ���ֲ�ֱ��ͼ����������
![]() ��2������������ͨ��ʱ����������9���ӵ�Ƶ�ʣ�
��2������������ͨ��ʱ����������9���ӵ�Ƶ�ʣ�
��3�������Сǿ����1000��ͨ������ͨ��ʱ��������15���ӵĴ�����