题目内容
【题目】(1)已知一次函数y=kx+b的图象经过A(0,1),B(2,0)两点,则当x_____时,y≤0.
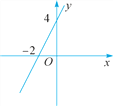
(2)如图是一次函数y=kx+b的图象,则关于x的不等式kx+b>0的解为______.
(3)若y关于x的一次函数y=mx+n的图象不经过第四象限,则m____0,n____0.
(4)设正比例函数y=mx的图象经过点A(m,4),且函数值y随x的增大而减小,则m=____.
【答案】 ≥2 x>-2 > ≥ -2
【解析】(1)∵一次函数y=kx+b的图象经过两点A(0,1),B(2,0),
∴![]() ,
,
∴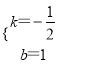
这个一次函数的表达式为y=- ![]() +1,
+1,
- ![]() +1≤0,
+1≤0,
解得x≥2;
(2)由图可知:当x>-2时,y>0,即kx+b>0;
因此kx+b>0的解集为:x>-2.
(3):∵一次函数y=mx+n的图形不经过第四象限,
∴m>0,
当此函数图象经过原点时,n=0;
当此函数图象不经过原点时,n>0.
故答案为>,≥.
(4)把x=m,y=4代入y=mx中,
可得:m=±2,
因为y的值随x值的增大而减小,
所以m=-2.
故答案是: ≥2,x>-2 , > ,≥, -2.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目