题目内容
【题目】在四边形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是射线
是射线![]() 上一动点,以
上一动点,以![]() 为边向右侧作等边
为边向右侧作等边![]() ,点
,点![]() 的位置随着点
的位置随着点![]() 的位置变化而变化.
的位置变化而变化.

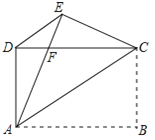
(1)如图1,当点![]() 在四边形
在四边形![]() 内部或边上时,连接
内部或边上时,连接![]() ,
,![]() 与
与![]() 的数量关系是________,
的数量关系是________,![]() 与
与![]() 的位置关系是_______;
的位置关系是_______;
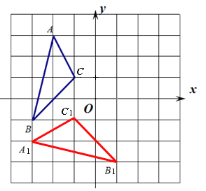
(2)如图2,当点![]() 在四边形
在四边形![]() 外部时,(1)中的结论是否还成立?若成立,请予以证明;
外部时,(1)中的结论是否还成立?若成立,请予以证明;
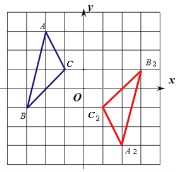
(3)如图3,当点![]() 在线段
在线段![]() 的延长线上时,连接
的延长线上时,连接![]() ,若
,若![]() ,
,![]() ,则线段
,则线段![]() ______,
______,![]() ________.
________.
【答案】(1)PB=EC,CE⊥AD;(2)结论仍然成立,理由见解析;(3)DP= 10,EP=![]()
【解析】
(1)如图1中,结论:PB=EC,CE⊥AD.连接AC,延长CE交AD于H,根据“SAS”证明△BAP≌△CAE即可解决问题;
(2)结论仍然成立.连接AC交BD于O,设CE交AD于H.证明方法与(1)类似;
(3)首先证明△BAP≌△CAE,解直角三角形求出AP,DP,OA即可解决问题;
解:(1)如图1中,结论:PB=EC,CE⊥AD.
理由:连接AC,延长CE交AD于H.
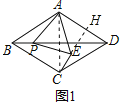
∵四边形ABCD是菱形,∠ABC=60°,
∴△ABC,△ACD都是等边三角形,∠ABD=∠CBD=30°,
∴AB=AC,∠BAC=60°,
∵△APE是等边三角形,
∴AP=AE,∠PAE=60°,
∵∠BAC=∠PAE,
∴∠BAP=∠CAE,
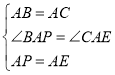 ,
,
∴△BAP≌△CAE,
∴BP=CE,∠ABP=∠ACE=30°,
∵∠CAH=60°,
∴∠CAH+∠ACH=90°,
∴∠AHC=90°,即CE⊥AD.
故答案为PB=EC,CE⊥AD;
(2)结论仍然成立.
理由:选图2,连接AC交BD于O,设CE交AD于H.
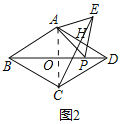
∵四边形ABCD是菱形,∠ABC=60°,
∴△ABC,△ACD都是等边三角形,∠ABD=∠CBD=30°,
∴AB=AC,∠BAC=60°,
∵△APE是等边三角形,
∴AP=AE,∠PAE=60°,
∴∠BAP=∠CAE.
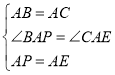 ,
,
∴△BAP≌△CAE,
∴BP=CE,∠PBA=∠ACE=30°,
∵∠CAH=60°,
∴∠CAH+∠ACH=90°,
∴∠AHC=90°,即CE⊥AD.
(3)选图3,连接AC交BD于O,连接CE交AD于H.
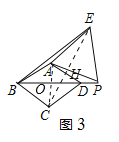
∵四边形ABCD是菱形,∠ABC=60°,
∴△ABC,△ACD都是等边三角形,∠ABD=∠CBD=30°,
∴AB=AC,∠BAC=60°,
∵△APE是等边三角形,
∴AP=AE,∠PAE=60°,
∴∠BAP=∠CAE.
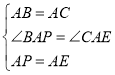 ,
,
∴△BAP≌△CAE,
∴BP=CE,∠ABP=∠ACE=30°,
∵∠CAH=60°,
∴∠CAH+∠ACH=90°,
∴∠AHC=90°,即CE⊥AD.
在菱形ABCD中,AD∥BC,
∴EC⊥BC,
∵BC=AB=2![]() ,BE=
,BE=![]() ,
,
在Rt△BCE中,EC=![]() =7,
=7,
∴BP=CE=7,
∵AC与BD是菱形的对角线,
∴∠ABD=![]() ∠ABC=30°,AC⊥BD,
∠ABC=30°,AC⊥BD,
∴OA=![]() AB=
AB=![]() ,
,
∴BO=OD=![]() =3,
=3,
∴BD=2BO=6,
∴DP=BP-BD=7-6=1,
∴OP=OD+DP=4,
在Rt△AOP中,AP=![]() ,
,
∴EP=AP=![]() .
.