Question

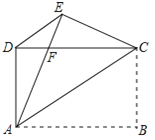
【题目】如图1，已如直线∥，且与、分别交于A、B两点，与、分别交于C、D两点，记∠ACP=∠1，∠BDP=∠2，∠CPD=∠3，点P在线段AB上.

(1)若∠1=25°，∠2=33°，则∠3=__________；

(2)猜想∠1，∠2，∠3之间的相等关系，并说明理由；

(3)如图2，点在点B的南偏东23°方向，在点C的西南方向，利用(2)的结论，可知∠BAC=__________；

(4)点P在直线上且在A、B两点外侧运动时，其它条件不变，请直接写出∠1，∠2，∠3之间的相等关系.

Answer 1

【答案】(1)58°；(2)∠1+∠2=∠3，理由见解析；(3)68°；(4)当点P在直线上且在上方运动时，∠1+∠3=∠2 ，当点P在直线上且在上方运动时，∠2+∠3=∠1

【解析】

（1）根据平行线的性质和三角形内角和定理即可求解；（2）∠1+∠2=∠3，作PQ∥，可得PQ∥∥，由平行线的性质可得∠1=∠CPQ，∠2=∠DPQ，即可得∠CPD=∠CPQ+∠DPQ=∠1+∠2；（3）过A点作AF∥BE，则AF∥BE∥CD，即可得∠BAC=∠EBA+∠ACD=23°+45°=68°；（4）分当点P在直线上且在上方运动时和点P在直线上且在的下方运动时两种情况，类比（2）的方法求解即可.

（1）∵l1∥l2，
∴∠1+∠PCD+∠PDC+∠2=180°，

在△PCD中，∠3+∠PCD+∠PDC=180°，

∴∠3=∠1+∠2=58°，

故答案为：58°；

(2)∠1+∠2=∠3

理由如下：

作PQ∥

∵∥，所以PQ∥∥(平行公理的推论)

∴∠1=∠CPQ，∠2=∠DPQ(两直线平行，内错角相等).

又∵∠CPD=∠CPQ+∠DPQ，

∴∠1+∠2=∠CPD(等量代换)；

(3) 过A点作AF∥BE，则AF∥BE∥CD，

则∠BAC=∠EBA+∠ACD=23°+45°=68°；

故答案为：68°；

(4)当点P在直线上且在上方运动时，∠1+∠3=∠2 ，

如图，过P作PF∥l1，交l4于F，

∴∠1=∠FPC．

∵l1∥l2，

∴PF∥l2，

∴∠2=∠FPD.

∵∠FPD = ∠FPC + ∠CPD,

∴∠2=∠3+∠1．

当点P在直线上且在的下方运动时，∠2+∠3=∠1,

过P作PG∥l2，交l4于G，
∴∠2=∠GPC，

∵l1∥l2，

∴PG∥l1，

∴∠1=∠DPG，

∵∠CPD+∠CPG=∠GPD,

∴∠1=∠2+∠3．