题目内容
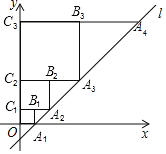
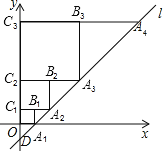
【题目】在平面直角坐标系xOy中，直线l：y＝2x﹣2与x轴交于点A1，如图所示，依次作正方形A1B1C1O，正方形A2B2C2C1，…，正方形AnBnnCn﹣1，使得点A1，A2，A3，…An在直线l上，点C1，C2，C3，…n在y轴正半轴上，则正方形AnBnnCn﹣1的面积是_____．
【答案】
【解析】
由直线点的特点得到
，分别可求OA1＝OC1＝1，C1A2＝
，C2A3＝
，……，从而得到正方形边长的规律为Cn﹣1An＝
，即可求正方形面积．
解：直线l：y＝2x﹣2与x轴交于点A（1，0），与y轴交于点D（0，﹣2），
∴，
∵OA1＝OC1＝1，
∴A1B1C1O的面积是1；
∴DC1＝3，
∴C1A2＝，
∴A2B2C2C1的面积是；
∴DC2＝
，
∴C2A3＝，
∴A3B3C3C2的面积是
；
……
∴Cn﹣1An＝，
∴正方形AnBnnCn﹣1的面积是，
故答案为．
练习册系列答案
全优冲刺100分系列答案
英才点津系列答案
相关题目
