Question

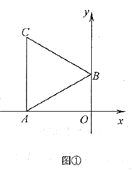
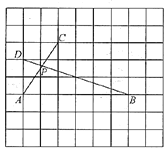
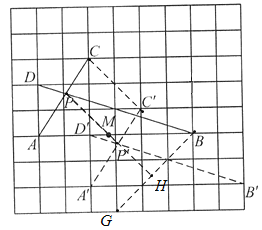
【题目】如图，在每个小正方形边长为1的网格中，点均在格点上，交于点．

(Ⅰ)的值为_____________；

(Ⅱ)若点在线段上，当取得最小值时，请在如图所示的网格中用无刻度的直尺，画出点，并简要说明点的位置是如何找到的(不要求证明)_____________．

Answer 1

【答案】(Ⅰ)；(Ⅱ)取格点，连接与相交，得点．连接，与相交，得点，点即为所求，图形见解析．

【解析】

（1）根据正切的定义，在Rt△ABD中直接计算得出结果；

（2）过B点在AB下方作∠ABQ=45°，将转化为M到BQ的距离，于是最小值转化为P到直线BQ的最小值问题，即P到BQ的垂线段长，利用ABCD四点沿右下45°方向平移作P点的对应点P’，即可得PP’⊥BQ，PP’交AB与M，即所求．

解：(Ⅰ)∵∠DAB=90°，

∴

故答案为：

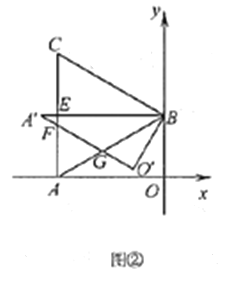
(Ⅱ)如图：取格点，连接与相交，得点．连接，与相交，得点，点即为所求．

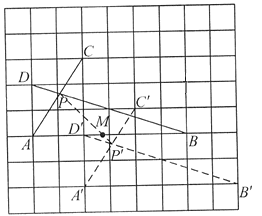
证明：如下图，将A、B、C、D四点分别向下平移2个单位，向右平移2个单位，得对应点格点，连接与相交，得点．连接、，

∴//,

取格点G，连接BG，

由格点图形可知，

∴，

作MH⊥BG，

∵∠MBG=45°，

∴，

∴，

即当P、M、H三点共线时取最小值，即时，

故：连接与相交，得点，点即为所求．