题目内容
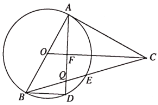
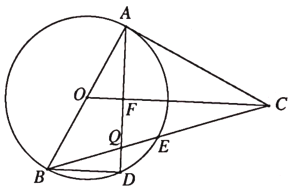
【题目】如图,AB是![]() 的直径,点E是
的直径,点E是![]() 的中点,CA与
的中点,CA与![]() 相切于点A交BE延长于点C,过点A作
相切于点A交BE延长于点C,过点A作![]() 于点F,交
于点F,交![]() 于点D,交BC于点Q,连接BD.
于点D,交BC于点Q,连接BD.
(1)求证:![]() ;
;
(2)若![]() ,求CQ的长.
,求CQ的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)根据直径可得∠ADB=90°,由E是弧AB的中点得∠ABE=45°,由相切的性质得∠BAC=90°,可推出△ABD≌△ACF ,即可得到结果.
(2)根据条件可证明△BDQ∽△CFQ,可得到![]() ,即可求出结果.
,即可求出结果.
证明:(1) ∵ AB是⊙O的直径,
![]() ∠ADB=90°,
∠ADB=90°,
∵点E是弧AB的中点,
![]() ∠ABE=45°,
∠ABE=45°,
∵CA与⊙O相切于点A,
![]() ∠BAC=90°,
∠BAC=90°,
![]() AB=AC,
AB=AC,
∵AD⊥OC于点F,
![]() ∠AFC=∠ADB=90°,
∠AFC=∠ADB=90°,
∵∠FAC+∠BAD=90°,∠FAC+∠ACF=90°,
![]() ∠BAD=∠ACF.
∠BAD=∠ACF.![]() △ABD≌△ACF,
△ABD≌△ACF,
∴BD=AF.
(2) ∵BD=2,
![]() AF=BD=2,
AF=BD=2,
∵AD⊥OC于点F,
![]() AD=2AF=4=CF,
AD=2AF=4=CF,
![]() Rt△ABD中,AB=
Rt△ABD中,AB=![]() ,
,
![]() Rt△ABC中,BC=
Rt△ABC中,BC=![]() ,
,
∵∠AFC=∠ADB=90°,∠FQC=∠DQB,
![]() △BDQ∽△CFQ,
△BDQ∽△CFQ,
![]()
![]() ,
,
![]() CQ=2BQ,
CQ=2BQ,
![]() CQ=
CQ=![]() .
.

练习册系列答案
相关题目