题目内容
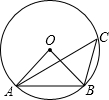 如图,点A、B、C都在⊙O上,且点C在弦AB所对的优弧上,若∠ABO=50°,则∠ACB的度数是
如图,点A、B、C都在⊙O上,且点C在弦AB所对的优弧上,若∠ABO=50°,则∠ACB的度数是
- A.20°
- B.30°
- C.40°
- D.50°
C
分析:在等腰△OAB中,已知了底角∠ABO的度数,根据三角形内角和定理即可得到顶角∠AOB的度数,由于∠AOB、∠ACB是同弧所对的圆心角和圆周角,根据圆周角定理即可得解.
解答:△AOB中,OA=OB,∠ABO=50°,则:
∠AOB=180°-2×50°=80°;
∴∠ACB= ∠AOB=40°,
∠AOB=40°,
故选C.
点评:此题主要考查的是等腰三角形的性质、三角形内角和定理以及圆周角定理的综合应用.
分析:在等腰△OAB中,已知了底角∠ABO的度数,根据三角形内角和定理即可得到顶角∠AOB的度数,由于∠AOB、∠ACB是同弧所对的圆心角和圆周角,根据圆周角定理即可得解.
解答:△AOB中,OA=OB,∠ABO=50°,则:
∠AOB=180°-2×50°=80°;
∴∠ACB=
 ∠AOB=40°,
∠AOB=40°,故选C.
点评:此题主要考查的是等腰三角形的性质、三角形内角和定理以及圆周角定理的综合应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
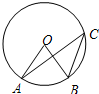 11、如图,点A、B、C都在⊙O上,若∠C=35°,则∠AOB=
11、如图,点A、B、C都在⊙O上,若∠C=35°,则∠AOB=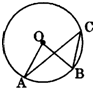 13、如图,点A、B、C都在00上,若∠C=40°,则∠AOB的度数为( )
13、如图,点A、B、C都在00上,若∠C=40°,则∠AOB的度数为( )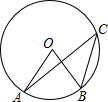 (2013•丰台区二模)如图,点A、B、C都在⊙O上,若∠AOB=68°,则∠ACB的度数为( )
(2013•丰台区二模)如图,点A、B、C都在⊙O上,若∠AOB=68°,则∠ACB的度数为( )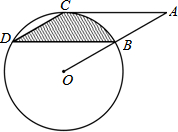 (2013•自贡)如图,点B、C、D都在⊙O上,过点C作AC∥BD交OB延长线于点A,连接CD,且∠CDB=∠OBD=30°,DB=
(2013•自贡)如图,点B、C、D都在⊙O上,过点C作AC∥BD交OB延长线于点A,连接CD,且∠CDB=∠OBD=30°,DB=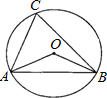 如图,点A、B、C都在⊙O上,连接AB、BC、AC、OA、OB,且∠BAO=25°,则∠ACB的大小为
如图,点A、B、C都在⊙O上,连接AB、BC、AC、OA、OB,且∠BAO=25°,则∠ACB的大小为