题目内容
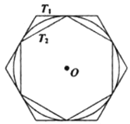
【题目】如图,有一个圆![]() 和两个正六边形
和两个正六边形![]() ,
,![]() .
.![]() 的6个顶点都在圆周上,
的6个顶点都在圆周上,![]() 的6条边都和圆
的6条边都和圆![]() 相切(我们称
相切(我们称![]() ,
,![]() 分别为圆
分别为圆![]() 的外切正六边形和内接正六边形),若设
的外切正六边形和内接正六边形),若设![]() ,
,![]() 的周长分别为
的周长分别为![]() ,
,![]() ,圆
,圆![]() 的半径为
的半径为![]() ,则
,则![]() ___;
___;![]() ____;正六边形
____;正六边形![]() ,
,![]() 的面积比
的面积比![]() 的值是____.
的值是____.
【答案】![]()
![]()
![]()
【解析】
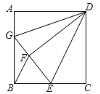
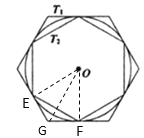
根据题意画出图形,连接OE、OG,OF,由正六边形T1,得到∠EOF为60°, 从而得到△EOF为等边三角形,即a=r, 故得到r:a=1:1;在Rt△EOG中,由OG为角平分线,得到∠EOG=30°,利用特殊角的三角函数可求出OE及OG的长,即为r:b的比值,然后求出a:b的比值,根据正六边形T1,T2相似,其面积之比等于边长之比的平方,即可求出面积之比.
连接OE、OG、OF,
∵![]() ,
,![]() 的周长分别为
的周长分别为![]() ,
,![]() ,
,
∴![]() ,
,![]() 的边长分别为
的边长分别为![]() ,
,![]() ,
,
∵EF=![]() ,且正六边形T2,
,且正六边形T2,
∴△OEF为等边三角形,OE为圆的半径r,
∴r:![]() = 1:1 ,
= 1:1 ,
∴r:b=![]() ;
;
由题意可知OG为∠FOE的平分线,即∠EOG= ![]() ∠EOF=30°,
∠EOF=30°,
在Rt△OEG中,OE=r,OG=![]() ,
,
∵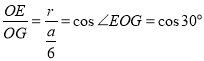 ,即
,即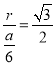 ,
,
∴r:a=![]() ;
;
∵r:b=![]() ,r:a=
,r:a=![]() ,
,
∴b:a=![]()
∵两个正六边形T1、T2相似,
∴![]() ,即
,即![]() ,
,
故答案为:![]() ,
,![]() ,
,![]() .
.

【题目】(问题)若a+b=10,则ab的最大值是多少?
(探究)
探究一:当a﹣b=0时,求ab值.
显然此时,a=b=5,则ab=5×5=25
探究二:当a﹣b=±1时,求ab值.
①a﹣b=1,则a=b+1,
由已知得b+1+b=10
解得 b=![]() ,
,
a=b+l=![]() +1=
+1=![]()
则ab=![]() =
=![]()
②a﹣b=﹣1,即b﹣a=1,由①可得,b=![]() ,a=
,a=![]()
则ab=![]() =
=![]() .
.
探究三:当a﹣b=±2时,求ab值(仿照上述方法,写出探究过程).
探究四:完成下表:
a﹣b | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
ab | … |
|
|
| 25 |
|
|
| … |
(结论)若a+b=10,则ab的最大值是 (观察上面表格,直接写出结果).
(拓展)若a+b=m,则ab的最大值是 .
(应用)用一根长为12m的铁丝围成一个长方形,这个长方形面积的最大值是 m2.