题目内容
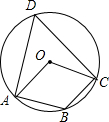 如图,A、B、C、D分别是⊙O上的四点,∠AOC=80°,则∠ADC和∠ABC等于
如图,A、B、C、D分别是⊙O上的四点,∠AOC=80°,则∠ADC和∠ABC等于
- A.40°和140°
- B.40°和110°
- C.50°和140°
- D.50°和110°
A
分析:根据圆周角定理求得∠ADC的度数,然后根据圆内接四边形的对角互补的性质来求∠ABC的度数.
解答:∵A、B、C、D分别是⊙O上的四点,
∴∠ADC= ∠AOC(同弧所对的圆周角是所对的圆心角的一半);
∠AOC(同弧所对的圆周角是所对的圆心角的一半);
∵∠AOC=80°,
∴∠ADC=40°;
又∠ADC+∠ABC=180°(圆内接四边形的对角互补),
∴∠ABC=140°.
故选A.
点评:本题综合考查了圆内接四边形的性质、圆周角定理.解答此题的关键点是利用圆周角定理求得圆周角∠ADC的度数,然后由圆内接四边形的对角互补的性质求得∠ABC的度数的.
分析:根据圆周角定理求得∠ADC的度数,然后根据圆内接四边形的对角互补的性质来求∠ABC的度数.
解答:∵A、B、C、D分别是⊙O上的四点,
∴∠ADC=
 ∠AOC(同弧所对的圆周角是所对的圆心角的一半);
∠AOC(同弧所对的圆周角是所对的圆心角的一半);∵∠AOC=80°,
∴∠ADC=40°;
又∠ADC+∠ABC=180°(圆内接四边形的对角互补),
∴∠ABC=140°.
故选A.
点评:本题综合考查了圆内接四边形的性质、圆周角定理.解答此题的关键点是利用圆周角定理求得圆周角∠ADC的度数,然后由圆内接四边形的对角互补的性质求得∠ABC的度数的.

练习册系列答案
相关题目
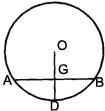 14、如图,已知⊙P的半径OD=5,OD⊥AB,垂足是G,OG=3,则弦AB=
14、如图,已知⊙P的半径OD=5,OD⊥AB,垂足是G,OG=3,则弦AB=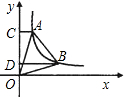 如图,已知A,B两点是反比例函数y=
如图,已知A,B两点是反比例函数y=

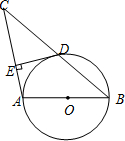 如图AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.
如图AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.