题目内容
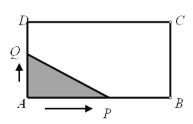
【题目】如图1,平行四边形ABCD中,AB⊥AC,AB=6,AD=10,点P在边AD上运动,以P为圆心,PA为半径的⊙P与对角线AC交于A,E两点.
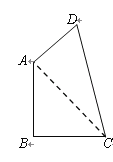
(1)如图2,当⊙P与边CD相切于点F时,求AP的长;
(2)不难发现,当⊙P与边CD相切时,⊙P与平行四边形ABCD的边有三个公共点,随着AP的变化,⊙P与平行四边形ABCD的边的公共点的个数也在变化,若公共点的个数为4,直接写出相对应的AP的值的取值范围 .

【答案】(1)AP=![]() ;(2)
;(2)![]() <AP<
<AP<![]() 或AP=5.
或AP=5.
【解析】
(1)如图2所示,连接PF,在Rt△ABC中,利用勾股定理求出AC=8,设AP=x,则DP=10﹣x,PF=x,由⊙P与边CD相切于点F,根据已知可推导得出△DPF∽△DAC,根据相似三角形对应边成比例即可求得AP长;
(2)当⊙P与BC相切时,设切点为G,如图3,利用面积法求出PG=![]() ,然后分两种情况①⊙P与边AD、CD分别有两个公共点,②⊙P过点A、C、D三点,分别讨论即可得.
,然后分两种情况①⊙P与边AD、CD分别有两个公共点,②⊙P过点A、C、D三点,分别讨论即可得.
(1)如图2所示,连接PF,
在Rt△ABC中,由勾股定理得:AC=![]() =8,
=8,
设AP=x,则DP=10﹣x,PF=x,
∵⊙P与边CD相切于点F,
∴PF⊥CD,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∵AB⊥AC,
∴AC⊥CD,
∴AC∥PF,
∴△DPF∽△DAC,
∴![]() ,
,
∴![]() ,
,
∴x=![]() ,即AP=
,即AP=![]() ;
;
(2)当⊙P与BC相切时,设切点为G,如图3,
SABCD=![]() ×6×8×2=10PG,
×6×8×2=10PG,
PG=![]() ,
,
①当⊙P与边AD、CD分别有两个公共点时,![]() <AP<
<AP<![]() ,即此时⊙P与平行四边形ABCD的边的公共点的个数为4,
,即此时⊙P与平行四边形ABCD的边的公共点的个数为4,
②⊙P过点A、C、D三点,如图4,⊙P与平行四边形ABCD的边的公共点的个数为4,
此时AP=5,
综上所述,AP的值的取值范围是:![]() <AP<
<AP<![]() 或AP=5.
或AP=5.
故答案为:![]() <AP<
<AP<![]() 或AP=5.
或AP=5.

 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案