题目内容
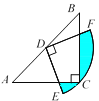
【题目】如图,在△ABC中,CA=CB,∠ACB=90°,AB=4,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为______________
【答案】π—2
【解析】
连接CD,作DM⊥BC,DN⊥AC,证明△DMG≌△DNH,则S四边形DGCH=S四边形DMCN,求得扇形FDE的面积,则阴影部分的面积即可求得.
解:连接CD,作DM⊥BC,DN⊥AC.
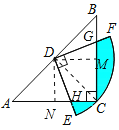
∵CA=CB,∠ACB=90°,点D为AB的中点,
∴DC=![]() AB=2,四边形DMCN是正方形,DM=
AB=2,四边形DMCN是正方形,DM=![]() .
.
则扇形FDE的面积是:![]() =π.
=π.
∵CA=CB,∠ACB=90°,点D为AB的中点,
∴CD平分∠BCA,
又∵DM⊥BC,DN⊥AC,
∴DM=DN,
∵∠GDH=∠MDN=90°,
∴∠GDM=∠HDN,
在△DMG和△DNH中,
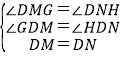
∴△DMG≌△DNH(AAS),
∴S四边形DGCH=S四边形DMCN=2
则阴影部分的面积是:π—2.

练习册系列答案
相关题目