题目内容
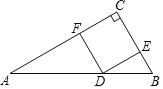
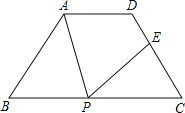
【题目】如图,在△ABC中,D是BC的中点,E是AD的中点,过点A作AF∥BC,AF与CE的延长线相交于点F,连接BF.

(1)求证:四边形AFBD是平行四边形;
(2)将下列命题填写完整,并使命题成立(图中不再添加其它的点和线):
①当△ABC满足条件AB=AC时,四边形AFBD是 形;
② 当△ABC满足条件 时,四边形AFBD是正方形.
【答案】(1)证明见解析;(2)① 矩形;②⊿ABC是等腰直角三角形.
【解析】
试题本题主要考查各种四边形的判定,基础题要细心.(1)要证明四边形AFBD是平行四边形一组对边平行且相等;(2)①矩形的对角线相等,②正方形对角线相等且垂直.
试题解析:(1)∵AF∥BC
∴∠AFE=∠ECD,∠FAE=∠CDE
又∵E是AD的中点
∴AE=DE
∴⊿AEF≌⊿DEC
∴AF=DC
又∵D是BC的中点
∴DB=DC
∴AF=DB
又∵AF∥BC
∴四边形AFBD是平行四边形
(2)①矩形;②⊿ABC是等腰直角三角形.

练习册系列答案
相关题目