题目内容
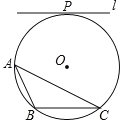
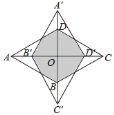
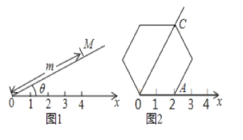
【题目】阅读理如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”。应用:在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点C的极坐标应记为___.
【答案】(60°,4).
【解析】
设正六边形的中心为D,连接AD,判断出△AOD是等边三角形,根据等边三角形的性质可得OD=OA,∠AOD=60°,再求出OC,然后根据“极坐标”的定义写出即可.
如图,设正六边形的中心为D,连接AD,
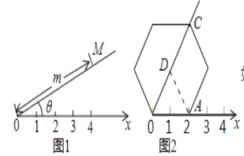
∵∠ADO=360°÷6=60°,OD=AD,
∴△AOD是等边三角形,
∴OD=OA=2,∠AOD=60°,
∴OC=2OD=2×2=4,
∴正六边形的顶点C的极坐标应记为(60°,4).
故答案为(60°,4).

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目