题目内容
【题目】如图,⊙O是△ABC的外接圆,半径为4,直线l与⊙O相切,切点为P,l∥BC,l与BC间的距离为7.
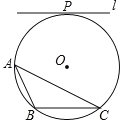
(1)仅用无刻度的直尺,画出一条弦,使这条炫将△ABC分成面积相等的两部分(保留作图痕迹,不写画法).
(2)求弦BC的长.
【答案】(1)画图见解析;(2)2![]() .
.
【解析】
试题分析:(1)连结PO并延长交BC于Q,然后连结AQ并延长交⊙O于D,则弦AD为所求;
(2)连结OC,如图,根据切线的性质得OP⊥l,则根据平行线的性质得PQ⊥BC,则根据垂径定理得BQ=CQ,然后在Rt△OCQ中利用勾股定理计算出CQ,则利用BC=2CQ求解.
试题解析:(1)如图,
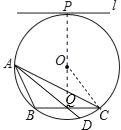
(2)连结OC,如图,
∵直线l与⊙O相切,切点为P,
∴OP⊥l,
而l∥BC,
∴PQ⊥BC,
∴BQ=CQ,
∵PQ=7,OP=OC=4,
∴OQ=3,
在Rt△OCQ中,CQ=![]() ,
,
∴BC=2CQ=2![]() .
.

练习册系列答案
相关题目