题目内容
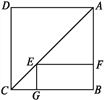
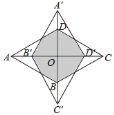
【题目】如图,菱形ABCD的一个内角是60,将它绕对角线的交点O顺时针旋转90后得到菱形A′B′C′D′.旋转前后两菱形重叠部分多边形的周长为![]() ,则菱形ABCD的边长为_________.
,则菱形ABCD的边长为_________.
【答案】2
【解析】
根据已知可得重叠部分是个八边形,根据其周长从而可求得其一边长即可得到答案.
因为旋转前后两菱形重叠部分多边形的周长为![]() ,
,
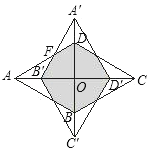
∴根据旋转的性质可得阴影部分为各边长相等的八边形,
∴B′F=FD=![]() ,
,
∵菱形ABCD的一个内角是60°,将它绕对角线的交点O顺时针旋转90后得到菱形A′B′C′D′,
∴∠DAO=∠B′A′O=30°,
∴∠A′B′C=60°,
∴∠AFB′=∠A′B′C-∠DAO=30°,
∴AB′=B′F=FD=![]() ,
,
∵DO=OB′=![]() AD,AO=
AD,AO=![]() AD,
AD,
∴AO=AB′+OB′=![]() +
+![]() AD,
AD,
∴![]() AD=
AD=![]() +
+![]() AD,
AD,
∴AD=2,
故答案为:2.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目