题目内容
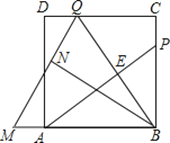
【题目】如图,点 O 是等边△ABC 内一点,∠AOB=105°,∠BOC 等于α,将△BOC 绕点 C 按 顺时针方向旋转 60°得△ADC,连接 OD.
(1)求证:△COD 是等边三角形.
(2)求∠OAD 的度数.
(3)探究:当α为多少度时,△AOD 是等腰三角形?

【答案】(1)证明见解析;(2)45°;(3)105°,127.5°或 150°.
【解析】(1)由旋转的性质得到△BCO≌△ACD, 再由全等三角形对应边相等得到OC=CD,根据有一个角为60°的等腰三角形是等边三角形即可得出结论;
(2)由等边三角形的性质、三角形内角和定理以及旋转的性质即可得出结论.
(3)若△AOD 是等腰三角形 ,分三种情况讨论即可.
(1)∵△BOC 旋转 60°得到△ADC,∴△BCO≌△ACD,
∴OC=CD,且∠OCD=60°,则△OCD 是等边三角形;
(2)∵△ABC 为等边三角形,∴∠BAO+∠OAC=60°,∠ABO+∠OBC=60°.
∵∠AOB=105°,∴∠BAO+∠ABO=75°,∴∠OAC+∠OBC=120°﹣105°=45°.
∵△BOC 旋转 60°得到△ADC,∴△BCO≌△ACD,
∴∠DAC=∠OBC ,∴∠OAD=∠OAC+∠CAD=45°.
(3)若△AOD 是等腰三角形 .∵由(1)知△OCD 是等边三角形,∴∠COD=60°.
由(2)知∠OAD=45°, 分三种情况讨论:
①当 OA=OD 时,∠AOD=90°,∠α=360°﹣105°﹣60°﹣90°=105°;
②当 OA=AD 时,∠AOD=67.5°,∠α=360°﹣105°﹣60°﹣67.5°=127.5°;
③当 AD=OD 时,∠AOD=45°,∠α=360°﹣105°﹣60°﹣45°=150°.
综上所述:当α=105°,127.5°或 150°时,△AOD 是等腰三角形 .