题目内容
【题目】探究规律：我们有可以直接应用的结论：若两条直线平行，那么在一条直线上任取一点，无论这点在直线的什么位置，这点到另一条直线的距离均相等.例如：如图1，两直线
∥
，两点
，
在上，
⊥于
，
⊥于
，则
.
如图2，已知直线∥，
，
为直线上的两点，
.
为直线上的两点.
（1）请写出图中面积相等的各对三角形： .
（2）如果，，为三个定点，点在上移动，那么无论点移动到任何位置，总有： 与
的面积相等；理由是： .
解决问题：
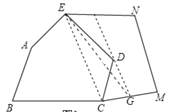
如图3，五边形
是张大爷十年前承包的一块土地的示意图，经过多年开垦荒地，现已变成如图4所示的形状，但承包土地与开垦荒地的分界小路（图4中折线
）还保留着，张大爷想过点修一条直路，直路修好后，要保持直路左边的土地面积与承包时的一样多.请你用以上的几何知识，按张大爷的要求设计出修路方案.（不计分界小路与直路的占地面积）
（1）写出设计方案，并在图4中画出相应的图形；
（2）说明方案设计理由.
【答案】探究规律：（1）
和
，
和
，
和
；（2）； 同底等高的两个三角形的面积相等；解决问题：（1）方案见解析；（2）理由见解析.
【解析】分析：(1)根据同底等高的三角形的面积相等与三角形的面积的和差关系求解；(2)①结合三角形的面积公式回答；②根据平行线间的距离处处相等和同底等高的两三角形面积相等设计方案.
详解：(1)和，和，和.
(2)；同底等高的两个三角形的面积相等.
连接
，过
点作的平行线
交
于点
，连接
，
就是所求的道路.
设EF交CD于点H，
∵EC∥DF，
∴D和F点到EC的距离相等(平行线间的距离处处相等)，
又∵EC＝EC，
∴S△ECF＝S△ECD(同底等高的两三角形面积相等)，
∴S五边形ABCDE＝S五边形EDCMN，S五边形EDCMN＝S四边形EFMN．
即：EF为直路的位置可以保持直路左边的土地面积与承包时的一样多，右边的土地面积与开垦的荒地面积一样多
