题目内容
一张等腰直角三角形纸片ABC,∠A=90°,AB=AC=2
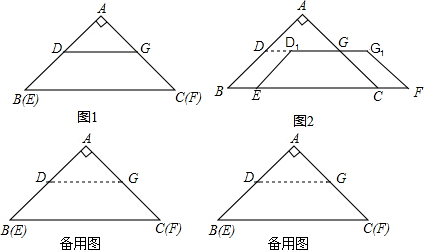
,另有一张等腰梯形纸片DEFG,DG∥EF,DE=GF.现将两张纸片叠放在一起(如图1),此时梯形的下底EF与BC边完全重合,梯形的两腰分别落在AB,AC上,且D,G恰好分别是AB,AC的中点.
(1)求BC的长及等腰梯形DEFG的面积;
(2)实验与探究(备用图供实验、探究使用)
如图2,固定△ABC,将等腰梯形DEFG以每秒1厘米的速度沿射线BC方向平行移动,宜到点E与点C重合时停止,设运动时间为x秒时,等腰梯形平移到D1EFG1的位置.
①当x为何值时,四边形DBED1是菱形,并说明理由.
②设△ABC与等腰梯形D1EFG1重叠部分的面积为y,直接写出y与x之间的函数关系式.
| 2 |
(1)求BC的长及等腰梯形DEFG的面积;
(2)实验与探究(备用图供实验、探究使用)
如图2,固定△ABC,将等腰梯形DEFG以每秒1厘米的速度沿射线BC方向平行移动,宜到点E与点C重合时停止,设运动时间为x秒时,等腰梯形平移到D1EFG1的位置.
①当x为何值时,四边形DBED1是菱形,并说明理由.
②设△ABC与等腰梯形D1EFG1重叠部分的面积为y,直接写出y与x之间的函数关系式.

分析:(1)在Rt△ABC中,由勾股定理求出BC=4,根据三角形中位线求出DG=
BC=2,BD=
AB=
,过D作DM⊥BC于M,求出DM,根据面积公式求出即可.
(2)①当x=
秒时,四边形DBED1是菱形,求出四边形DBED1是平行四边形,根据菱形的判定得出BE=DB=
.
②分为两种情况:画出图形,(i)当0<x≤2时,则DM=1,D1G=2-x,CE=4-x,根据面积公式求出即可.(ii)当2<x≤4时,点D1在线段DG的延长线上时,
设D1E和CG交于N,过N作NH⊥BC于H,求出EC=4-x,求出CN=NE=
,根据三角形面积公式求出即可.
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
(2)①当x=
| 2 |
| 2 |
②分为两种情况:画出图形,(i)当0<x≤2时,则DM=1,D1G=2-x,CE=4-x,根据面积公式求出即可.(ii)当2<x≤4时,点D1在线段DG的延长线上时,
设D1E和CG交于N,过N作NH⊥BC于H,求出EC=4-x,求出CN=NE=
| 4-x | ||
|
解答:解:(1)在Rt△ABC中,∠BAC=90°,AB=AC=2
,由勾股定理得:BC=
=4,
∴∠B=45°,EF=BC=4,
∵D、G分别是AB、AC的中点,
∴DG=
BC=2,BD=
AB=
,
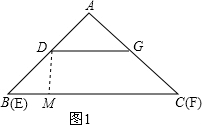 过D作DM⊥BC于M,如图1,
过D作DM⊥BC于M,如图1,
则∠DMB=90°,
∵∠B=45°,BD=2,
∴DM=BM=1,
∴S梯形DEFG=
×(DG+EF)×DM=
×(2+4)×1=3.
(2)①如图2,当x=
秒时,四边形DBED1是菱形,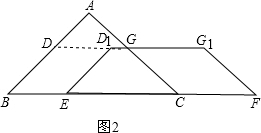
理由是:根据题意BE=x,
∵BD∥ED1,DD1∥BE,
∴四边形DBED1是平行四边形,
当BE=DB=
时,四边形DBED1为菱形.
②分为两种情况:
(i)、如图3,当0<x≤2时,
点D1在线段DG上,
DM=1,D1G=2-x,CE=4-x,
则重叠部分的面积是y=
•(2-x+4-x)•1,
即y=3-x;
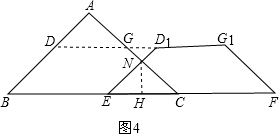
(ii)、当2<x≤4时,点D1在线段DG的延长线上时,如图4,
设D1E和CG交于N,过N作NH⊥BC于H,
 ∵平移得到四边形D1EFG1,
∵平移得到四边形D1EFG1,
∴∠ENC=∠A=90°,
∵EC=4-x,∠NCE=45°,
∴∠NEC=45°=∠NCE,
∴CN=NE=
,
∴重叠部分的面积y=
×CN×NE=
•
•
,
即y=
x2-2x+4.
| 2 |
| AB2+AC2 |
∴∠B=45°,EF=BC=4,
∵D、G分别是AB、AC的中点,
∴DG=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
 过D作DM⊥BC于M,如图1,
过D作DM⊥BC于M,如图1,则∠DMB=90°,
∵∠B=45°,BD=2,
∴DM=BM=1,
∴S梯形DEFG=
| 1 |
| 2 |
| 1 |
| 2 |
(2)①如图2,当x=
| 2 |

理由是:根据题意BE=x,
∵BD∥ED1,DD1∥BE,
∴四边形DBED1是平行四边形,
当BE=DB=
| 2 |
②分为两种情况:
(i)、如图3,当0<x≤2时,

点D1在线段DG上,
DM=1,D1G=2-x,CE=4-x,
则重叠部分的面积是y=
| 1 |
| 2 |
即y=3-x;
(ii)、当2<x≤4时,点D1在线段DG的延长线上时,如图4,
设D1E和CG交于N,过N作NH⊥BC于H,
 ∵平移得到四边形D1EFG1,
∵平移得到四边形D1EFG1,∴∠ENC=∠A=90°,
∵EC=4-x,∠NCE=45°,
∴∠NEC=45°=∠NCE,
∴CN=NE=
| 4-x | ||
|
∴重叠部分的面积y=
| 1 |
| 2 |
| 1 |
| 2 |
| 4-x | ||
|
| 4-x | ||
|
即y=
| 1 |
| 4 |
点评:本题考查了三角形的面积,菱形的性质和判定,勾股定理,平行线的性质,梯形的性质,三角形的中位线性质的应用,主要考查学生综合运用性质进行计算的能力,有一定的难度.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
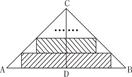
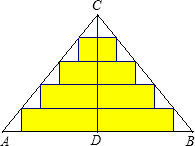 如图,△ABC是一张等腰直角三角形彩色纸,AC=BC=40cm.
如图,△ABC是一张等腰直角三角形彩色纸,AC=BC=40cm.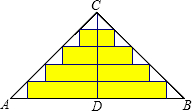 如图△ABC是一张等腰直角三角形彩色纸,AC=BC=20cm.将斜边上的高CD五等分,然后裁出4张宽度相等的长方形纸条.这4张小长方形的面积和
如图△ABC是一张等腰直角三角形彩色纸,AC=BC=20cm.将斜边上的高CD五等分,然后裁出4张宽度相等的长方形纸条.这4张小长方形的面积和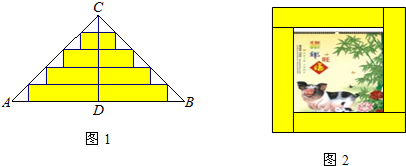
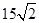 cm,∠ACB=90°现要沿AB边向上依次截取宽度均为2cm的长方形纸条,如图所示.已知截得的长方形纸片中有一块是正方形,则这块正方形纸片是( )
cm,∠ACB=90°现要沿AB边向上依次截取宽度均为2cm的长方形纸条,如图所示.已知截得的长方形纸片中有一块是正方形,则这块正方形纸片是( )