题目内容
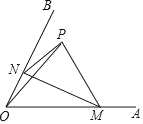
【题目】如图,∠AOB=60°,点P是∠AOB内的定点且OP=![]() ,若点M、N分别是射线OA、OB上异于点O的动点,则△PMN周长的最小值是( )
,若点M、N分别是射线OA、OB上异于点O的动点,则△PMN周长的最小值是( )
A. ![]() B.
B. ![]() C. 6 D. 3
C. 6 D. 3
【答案】D
【解析】作P点分别关于OA、OB的对称点C、D,连接CD分别交OA、OB于M、N,如图,利用轴对称的性质得MP=MC,NP=ND,OP=OD=OC=![]() ,∠BOP=∠BOD,∠AOP=∠AOC,所以∠COD=2∠AOB=120°,利用两点之间线段最短判断此时△PMN周长最小,作OH⊥CD于H,则CH=DH,然后利用含30度的直角三角形三边的关系计算出CD即可.
,∠BOP=∠BOD,∠AOP=∠AOC,所以∠COD=2∠AOB=120°,利用两点之间线段最短判断此时△PMN周长最小,作OH⊥CD于H,则CH=DH,然后利用含30度的直角三角形三边的关系计算出CD即可.
作P点分别关于OA、OB的对称点C、D,连接CD分别交OA、OB于M、N,如图,
则MP=MC,NP=ND,OP=OD=OC=![]() ,∠BOP=∠BOD,∠AOP=∠AOC,
,∠BOP=∠BOD,∠AOP=∠AOC,
∴PN+PM+MN=ND+MN+MC=DC,∠COD=∠BOP+∠BOD+∠AOP+∠AOC=2∠AOB=120°,
∴此时△PMN周长最小,
作OH⊥CD于H,则CH=DH,
∵∠OCH=30°,
∴OH=![]() OC=
OC=![]() ,
,
CH=![]() OH=
OH=![]() ,
,
∴CD=2CH=3.
故选D.


练习册系列答案
相关题目






