题目内容
【题目】如图,平面直角坐标系xoy中,抛物线y=a(x+1)(x-9)经过A,B两点,四边形OABC
矩形,已知点A坐标为(0,6)。

(1) 求抛物线解析式;
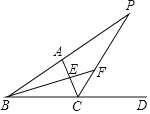
(2) 点E在线段AC上移动(不与C重合),过点E作EF⊥BE,交x轴于点F.请判断![]() 的值是否变化;若不变,求出它的值;若变化,请说明理由。
的值是否变化;若不变,求出它的值;若变化,请说明理由。
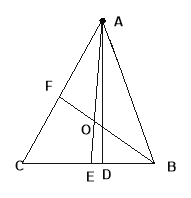
(3)在(2)的条件下,若E在直线AC上移动,当点E关于直线BF的对称点![]() 在抛物线对称轴上时,请求出BE的长度。
在抛物线对称轴上时,请求出BE的长度。
【答案】(1)![]() (2)不变 (3)
(2)不变 (3)![]()
【解析】分析(1) 将![]() 代入
代入![]() 即可求解;(2)由△BDE∽△EGF,得出
即可求解;(2)由△BDE∽△EGF,得出![]() ,由点A的坐标及对称轴直线x=4推出点B坐标,从而求解;(3) 过点E′作PQ∥x,易证△FPE′∽△BQE′,得出FP=3,利用CQ=3, BQ=9,求出BE即可得出结果.
,由点A的坐标及对称轴直线x=4推出点B坐标,从而求解;(3) 过点E′作PQ∥x,易证△FPE′∽△BQE′,得出FP=3,利用CQ=3, BQ=9,求出BE即可得出结果.
(1)将![]() 代入
代入![]() ,得:
,得:![]()
∴抛物线解析式为![]()
(2)![]() 的值不变.
的值不变.
如图,过点E作DG⊥AB交AB于点D,交![]() 轴于点G
轴于点G

∵四边形OABC为矩形, ∴DG⊥OC , BD=GC
由BE⊥EF, 易证△BDE∽△EGF, 得:![]() , 即
, 即![]() .
.
由![]() ,抛物线对称轴为直线
,抛物线对称轴为直线![]() ,得
,得![]() , 即OC=6.
, 即OC=6.
易知![]() , ∴
, ∴![]() .
.
(3)如图,过点E′作PQ∥x,FP⊥PQ, CQ⊥PQ.

易证△FPE′∽△BQE′.
可知QE′=4, ∴FP=3. 则CQ=3, BQ=9
∴BE=BE′=![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目