题目内容
【题目】某隧道洞的内部截面顶部是抛物线形,现测得地面宽 AB=10m,隧道顶点O到地面AB的距离为5m,
(1)建立适当的平面直角坐标系,幵求该抛物线的解析式;
(2)一辆小轿车长 4.5米,宽2米,高1.5米,同样大小的小轿车通过该隧道,最多能有 几辆车幵行?
【答案】(1)y=![]() x2;(2)4
x2;(2)4
【解析】
(1)以顶点为原点建立坐标系,待定系数法求函数解析式;(2)代入左端的车子最高点的的纵坐坐标,求横坐标.
(1)
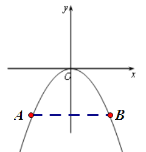
以O为原点建立坐标系,则A(-5,-5)、B(5,-5),
设抛物线的解析式为y=ax2,
把(-5,-5)代入,解得a=![]() ,
,
所以抛物线的解析式为y=![]() x2.
x2.
(2)当y=-5+1.5=-3.5时,x=±![]() .
.
能够开的车子数量为![]() ×2÷2=
×2÷2=![]() ≈4.
≈4.
所以能够开的车子的数量为4.

练习册系列答案
相关题目
【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销售量的相关信息如下表:
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200-2x | |
已知该商品的进价为每件30元,设销售该商品的每天利润为y元[
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.