题目内容
【题目】定义:若两个分式的和为![]() (
(![]() 为正整数),则称这两个分式互为“
为正整数),则称这两个分式互为“![]() 阶分式”,例如分式
阶分式”,例如分式![]() 与
与![]() 互为“3阶分式”.
互为“3阶分式”.
(1)分式![]() 与 互为“5阶分式”;
与 互为“5阶分式”;
(2)设正数![]() 互为倒数,求证:分式
互为倒数,求证:分式![]() 与
与![]() 互为“2阶分式”;
互为“2阶分式”;
(3)若分式![]() 与
与![]() 互为“1阶分式”(其中
互为“1阶分式”(其中![]() 为正数),求
为正数),求![]() 的值.
的值.
【答案】(1)![]() ;(2)详见解析;(3)
;(2)详见解析;(3)![]()
【解析】
(1)根据分式的加法,设所求分式为A,然后进行通分求解即可;
(2)根据题意首先利用倒数关系,将x,y进行消元,然后通过分式的加法化简即可得解;
(3)根据1阶分式的要求对两者相加进行分式加法化简,通过通分化简即可得解.
(1)依题意,所求分式为A,即:![]() ,
,
∴![]() ;
;
(2)∵正数![]() 互为倒数
互为倒数
∴![]() ,即
,即![]()
∴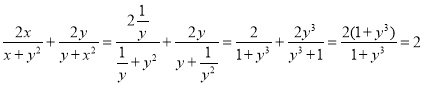
∴分式![]() 与
与![]() 互为“2阶分式”;
互为“2阶分式”;
(3)由题意得![]() ,等式两边同乘
,等式两边同乘![]()
化简得: ![]()
即:![]()
∴![]() ,即
,即![]()
∴![]() 或0
或0
∵![]() 为正数
为正数
∴![]() .
.

练习册系列答案
相关题目