Question

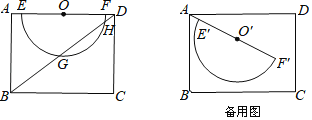
【题目】如图，矩形ABCD中，，，动点P从点A出发，在AC上以每秒5cm的速度向点C匀速运动，同时动点Q从点D出发，在DA边上以每秒4cm的速度向点A匀速运动，运动时间为t秒（），连接PQ.

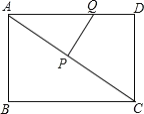
（1）若△APQ与△ADC相似，求t的值；

（2）连结CQ，DP，若，求t的值；

（3）连结BQ，PD，请问BQ能和PD平行吗？若能，求出t的值：若不能，说明理由.

Answer 1

【答案】（1）或；

（2）；

（3）不存在这样的t，理由见详解．

【解析】

1）根据相似三角形对应边成比例，即可得到结论；
（2）过P作PM⊥AD于M，根据相似三角形的性质列比例式求得PM=3t，AM=4t，MD=8-4t，根据已知条件推出△PMD∽△QDC，根据相似三角形的性质列方程即可得到结论；
（3）设DP交BC于N，根据相似三角形的性质列比例式求得，得到，当BQ∥DP，得到四边形BQDN是平行四边形，根据平行四边形的性质列方程即可得到结论．

解：（1）由题意得；QD=4t，AQ=8-4t，AP=5t，PC=10-t，
∵△APQ与△ADC相似，
∴情况①，当时，,

即： ，解得：；

情况②当时，,

即： ，解得：，

∴△APQ与△ADC相似时，或；

（2）

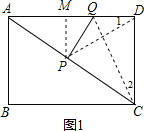
如图1，过P作PM⊥AD于M，

∵∠ADC=90°，

∴PM∥CD，

∴△APM∽△ACD，，

∴,

∵AP=5t，
∴

∴化简得出：PM=3t，AM=4t，MD=8-4t，
∵CQ⊥DP，∴∠1=∠2，
∵∠PMD=∠CDQ=90°，
∴△PMD∽△QDC，
∴,即：

解得：；

（3）

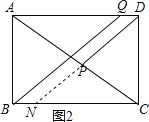
设DP交BC于N，

∴依题意得：，，
∵AD∥BC，
∴△ADP∽△CNP，

∴

∴，

∴，

当BQ∥DP，则四边形BQDN是平行四边形，
∴BN=QD，
即：

解得：，

当时，，，与题意不符，
∴不存在这样的t．