题目内容
【题目】如图,AD=AE,BE=CD,∠ADB=∠AEC=110°,∠BAE=80°,下列说法:①△ABE≌△ACD;②△ABD≌△ACE;③∠DAE=40°;④∠C=40°.其中正确的说法有( )

A.3个B.2个C.1个D.0个
【答案】A
【解析】
根据邻补角互补求出∠ADC=∠AEB=70°,根据三角形内角和定理即可判断③;根据全等三角形的判定定理即可判断①②;求出∠CAD的度数,根据三角形的内角和定理判断④即可.
∵∠ADB=∠AEC=110°,
∴∠ADC=∠AEB=180°﹣110°=70°,
∴∠DAE=180°﹣∠ADC﹣∠AEB=180°﹣70°﹣70°=40°,故③正确;
∵在△ABE和△ACD中
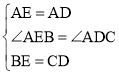
∴△ABE≌△ACD(SAS),故①正确;
∴∠B=∠C,∠BAE=∠CAD=80°,
∵在△ABD和△ACE中

∴△ABD≌△ACE(AAS),故②正确;
∵∠CAD=80°,∠ADC=70°,
∴∠C=180°﹣∠CAD﹣∠ADC=30°,故④错误;
即正确的个数是3个,
故选:A.

练习册系列答案
相关题目







